题目内容
若函数f(x)=|a|x2+x+1在[-1,+∞)上单调递增,则实数a的取值范围是 .
考点:二次函数的性质
专题:函数的性质及应用
分析:显然a可以等于0,而a≠0时,f(x)为二次函数,所以根据二次函数的单调性知-
≤-1,解出a再合并a=0即可得到a的取值范围.
| 1 |
| 2|a| |
解答:
解:若a=0,f(x)=x+1,满足在[-1,+∞)上单调递增;
若a≠0,则:-
≤-1,解得-
≤a≤
,且a≠0;
综上得a的取值范围为[-
,
].
故答案为:[-
,
].
若a≠0,则:-
| 1 |
| 2|a| |
| 1 |
| 2 |
| 1 |
| 2 |
综上得a的取值范围为[-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:[-
| 1 |
| 2 |
| 1 |
| 2 |
点评:考查一次函数的单调性,二次函数的单调性和对称轴的关系,解绝对值不等式.

练习册系列答案
相关题目
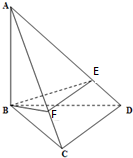 如图,在四面体ABCD中,AB⊥平面BCD,∠BCD=90°,点E是线段AD上一点(不与线段AD重合),F是点B在线段AC上的射影,求证:平面BEF⊥平面ACD.
如图,在四面体ABCD中,AB⊥平面BCD,∠BCD=90°,点E是线段AD上一点(不与线段AD重合),F是点B在线段AC上的射影,求证:平面BEF⊥平面ACD.