题目内容
已知数列{an}的通项公式为an=
+
+…+
(n∈N),求证:an是单调递增函数.
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
考点:数列的函数特性
专题:等差数列与等比数列
分析:根据通项公式得出n+1-an=
+
-
=
>0,可判断单调性.
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
| 1 |
| n+1 |
| 1 |
| (2n+1)(2n+2) |
解答:
解:∵列{an}的通项公式为an=
+
+…+
(n∈N),
∴an+1=
+
+…+
+
+
,
∴an+1-an=
+
-
=
>0,
即an+1>an,
∴数列{an}是单调递增数列.
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
∴an+1=
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
∴an+1-an=
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
| 1 |
| n+1 |
| 1 |
| (2n+1)(2n+2) |
即an+1>an,
∴数列{an}是单调递增数列.
点评:本题考查了根据数列的通项公式,作差an+1-an,判断正负,运用不等式求解,属于中档题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
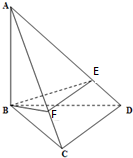 如图,在四面体ABCD中,AB⊥平面BCD,∠BCD=90°,点E是线段AD上一点(不与线段AD重合),F是点B在线段AC上的射影,求证:平面BEF⊥平面ACD.
如图,在四面体ABCD中,AB⊥平面BCD,∠BCD=90°,点E是线段AD上一点(不与线段AD重合),F是点B在线段AC上的射影,求证:平面BEF⊥平面ACD.