题目内容
4．
已知函数f（x）=||x|-2|+x-3．（1）画出y=f（x）的图象．
（2）解不等式f（x）＜$\frac{1}{2}$x+1．
分析 （1）根据解析式，画出y=f（x）的图象．
（2）利用图象，解不等式f（x）＜$\frac{1}{2}$x+1．
解答 解：（1）y=f（x）的图象，如图所示．
（2）由图象，可得不等式f（x）＜$\frac{1}{2}$x+1的解集为（-∞，4）．
点评 本题考查函数的图象的作法，绝对值不等式的解法，考查计算能力，考查数形结合的数学思想，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
12．在平面直角坐标系中，不等式组$\left\{\begin{array}{l}x≥0\\ x+y≤2\\ x≤y\end{array}\right.$所表示的平面区域的面积为（ ）
| A． | 1 | B． | 2 | C． | 4 | D． | 8 |
19．
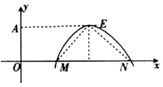已知奇函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的部分图象如图所示，点M的坐标为（1，0）且△MNE为等腰直角三角形，当A取最大值时，f（$\frac{1}{3}$）等于（ ）
已知奇函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的部分图象如图所示，点M的坐标为（1，0）且△MNE为等腰直角三角形，当A取最大值时，f（$\frac{1}{3}$）等于（ ）| A． | -$\frac{\sqrt{3}}{4}$ | B． | -$\frac{\sqrt{3}}{2}$ | C． | -$\frac{1}{2}$ | D． | -1 |
9．
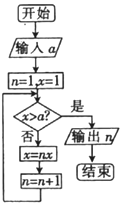执行如图所示程序框图，若输出的结果为5，则输入的实数a的范围是（ ）
执行如图所示程序框图，若输出的结果为5，则输入的实数a的范围是（ ）| A． | [6，24） | B． | [24，120） | C． | （-∞，6） | D． | （5，24） |
16．已知向量$\overrightarrow a=（cosθ，sinθ）$，向量$\overrightarrow{b}$=（$\sqrt{3}$，1），且$\overrightarrow{a}$⊥$\overrightarrow{b}$，则tanθ的值是（ ）
| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $-\frac{{\sqrt{3}}}{3}$ | C． | $\sqrt{3}$ | D． | -$\sqrt{3}$ |
13．某象棋俱乐部有队员5人，其中女队员2人，现随机选派2人参加象棋比赛，则选出的2人中恰有1人是女队员的概率为（ ）
| A． | $\frac{3}{10}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{2}{3}$ |