Question

19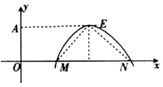．已知奇函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的部分图象如图所示，点M的坐标为（1，0）且△MNE为等腰直角三角形，当A取最大值时，f（$\frac{1}{3}$）等于（　　）

• A． -$\frac{\sqrt{3}}{4}$
• B． -$\frac{\sqrt{3}}{2}$
• C． -$\frac{1}{2}$
• D． -1

Answer 1

分析 根据f（x）=Acos（ωx+φ）（A＞0，ω＞0，0＜φ＜π）是奇函数，可得f（0）=0，求出φ=$\frac{π}{2}$，
根据图象过点M的坐标为（1，0）求出ω和E的坐标，根据A取最大值时，确定ω的值．可得f（x）解析式，从而求解f（$\frac{1}{3}$）的值．

解答 解：由题意，f（x）=Acos（ωx+φ）（A＞0，ω＞0，0＜φ＜π）是奇函数，可得f（0）=0，
∴φ=$\frac{π}{2}$，
可得f（x）=-Asinωx，
其周期T=$\frac{2π}{ω}$．
∵图象过点M的坐标为（1，0），
可得sinω=0，
那么ω=kπ，k∈Z，
由三角函数性质可得：E的坐标为（1+$\frac{π}{2ω}$，A）
∵△MNE为等腰直角三角形，
∴A=$\frac{π}{2ω}$，
又∵ω＞0，
当k=1时，ω取得最小值为π，此时A最大为$\frac{π}{2π}=\frac{1}{2}$．
∴函数f（x）=-$\frac{1}{2}$sinπx；
那么f（$\frac{1}{3}$）=$-\frac{1}{2}$sin$\frac{π}{3}$=$-\frac{\sqrt{3}}{4}$．
故选A．

点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用，f（x）是奇函数，可得f（0）=0，
求出E的坐标为（1+$\frac{π}{2ω}$，A）是解决本题的关键．属于中档题．