题目内容
13.己知命题p:方程$\frac{{x}^{2}}{12-m}$+$\frac{{y}^{2}}{m-4}$=1表示焦点在x轴上的椭圆;命题q:点(m,3)在圆(x-10)2+(y-1)2=13内.若p∨q为真命题,p∧q为假命题,试求实数m的取值范围.分析 先求出命题p,q为真命题的等价条件,然后根据若p∨q为真命题,p∧q为假命题,得到命题p,q为一真一假,然后求出实数m的取值范围.
解答 解:方程$\frac{{x}^{2}}{12-m}$+$\frac{{y}^{2}}{m-4}$=1表示焦点在x轴上的椭圆,则$\left\{\begin{array}{l}{12-m>0}\\{m-4>0}\\{12-m>m-4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m<12}\\{m>4}\\{m<8}\end{array}\right.$,即4<m<8.即p:4<m<8.
若(m,3)在圆(x-10)2+(y-1)2=13,则$\sqrt{(m-10)^{2}+(3-1)^{2}}$<$\sqrt{13}$,
即(m-10)2<9,即-3<m-10<3,所以7<m<13.即q:7<m<13.
若p∨q为真命题,p∧q为假命题,得到命题p,q为一真一假,
若p真q假,则$\left\{\begin{array}{l}{4<m<8}\\{m≥13或m≤7}\end{array}\right.$,解得4<m≤7.
若p假q真,则$\left\{\begin{array}{l}{m≥8或m≤4}\\{7<m<13}\end{array}\right.$,解得8≤m<13.
综上实数m的取值范围是4<m≤7或8≤m<13.
点评 本题主要考查复合命题真假判断,根据条件求出命题p,q为真命题时的等价条件是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知tanθ=$\frac{1}{2}$,则tan($\frac{π}{4}$-θ)=( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
1.对于常数m,n,“m>0,n>0”是“方程mx2-ny2=1的曲线是双曲线”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.己知圆M (x+1)2+y2=64,定点N(1,0),点P为圆M上的动点,点Q在NP上,点G在线段MP上,且满足$\overrightarrow{NP}$=2$\overrightarrow{NQ}$,$\overrightarrow{GQ}$•$\overrightarrow{NP}$=0,则点G的轨迹方程是( )
| A. | $\frac{{x}^{2}}{15}$+$\frac{{y}^{2}}{14}$=1 | B. | $\frac{{x}^{2}}{17}$+$\frac{{y}^{2}}{16}$=1 | C. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{15}$=1 | D. | $\frac{{x}^{2}}{14}$+$\frac{{y}^{2}}{13}$=1 |
5.“直线l的方程为y=k(x-2)”是“直线l经过点(2,0)”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
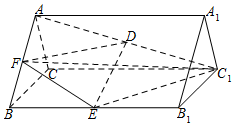 如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D,E分别为AC1和BB1的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D,E分别为AC1和BB1的中点. 已知抛物线E:y2=2px(P>0)的准线为x=-1,M,N为直线x=-2上的两点,M,N两点的纵坐标之积为-8,P为抛物线上一动点,PN,PM,分别交抛物线于A,B两点.
已知抛物线E:y2=2px(P>0)的准线为x=-1,M,N为直线x=-2上的两点,M,N两点的纵坐标之积为-8,P为抛物线上一动点,PN,PM,分别交抛物线于A,B两点.