题目内容
已知圆C的半径为2,圆心在x轴的正半轴上,直线3x+4y+4=0与圆C相切,则圆C的方程为 .
考点:圆的标准方程
专题:直线与圆
分析:直线与圆相切,设圆心坐标为(a,0),则圆方程为(x-a)2+y2=4,由已知得d=R=2=
,由此能求出圆C的方程.
| |3a+4×0+4| | ||
|
解答:
解:直线与圆相切,设圆心坐标为(a,0),
则圆方程为:
(x-a)2+y2=4,
∵圆心与切点连线必垂直于切线,
根据点与直线距离公式,得d=R=2=
,
解得a=2或a=-
,(因圆心在正半轴,不符合舍去)
∴a=2,
∴圆C的方程为:(x-2)2+y2=4.
故答案为:(x-2)2+y2=4.
则圆方程为:
(x-a)2+y2=4,
∵圆心与切点连线必垂直于切线,
根据点与直线距离公式,得d=R=2=
| |3a+4×0+4| | ||
|
解得a=2或a=-
| 14 |
| 3 |
∴a=2,
∴圆C的方程为:(x-2)2+y2=4.
故答案为:(x-2)2+y2=4.
点评:本题考查圆的方程的求法,解题时要认真审题,注意圆的方程的性质的合理运用.

练习册系列答案
相关题目
给出下列四个命题:①?x∈R,x是方程3x-5=0的根; ②?x∈R,|x|>0; ③?x∈R;x2≤0,④?x∈R,都不是方程x2-3x+3=0的根.其中真命题的序号是( )
| A、①④ | B、①③ |
| C、①③④ | D、②③④ |
曲线f(x)=ax3-3x+b在点(2,f(2))处的切线恰好是x轴,则a=( )
A、
| ||
B、
| ||
| C、1 | ||
| D、无法确定 |
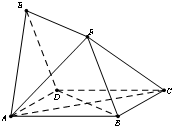 如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60,且FA=FC.
如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60,且FA=FC.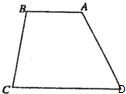 如图所示,有一块四边形的空、地,现欲把它绿化,需知道其面积,以便估算费用.现测得AB=5m,AD=CD=19m,BC=16m,∠ADC=60°.则这块四边形空地的面积是
如图所示,有一块四边形的空、地,现欲把它绿化,需知道其面积,以便估算费用.现测得AB=5m,AD=CD=19m,BC=16m,∠ADC=60°.则这块四边形空地的面积是 如图是函数y=f(x)的导函数f′(x)的图象,对下列四个命题:其中正确的命题是
如图是函数y=f(x)的导函数f′(x)的图象,对下列四个命题:其中正确的命题是