Question

已知正方体ABCD-A₁B₁C₁D₁的棱长为2，E，F分别是BB₁，DD₁的中点，求证：
（1）FC₁∥平面ADE；
（2）平面ADE∥平面B₁C₁F．

Answer 1

考点：向量方法证明线、面的位置关系定理,直线与平面平行的判定,平面与平面平行的判定

专题：空间位置关系与距离

分析：建立空间直角坐标系D-xyz，求出D，A，C，C₁，E，F，B₁，的坐标，求出

FC1

，

DA

，

AE

．
（1）利用向量的数量积为0求出平面ADE的法向量，通过向量的数量积推出

n1

⊥

FC1

，利用直线与平面平行的判定定理证明FC₁∥平面ADE．
（2）求出平面B₁C₁F的一个法向量．与平面ADE的法向量，通过向量共线证明，平面ADE∥平面B₁C₁F．

解答： 解：如图所示建立空间直角坐标系D-xyz，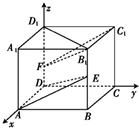
则有D（0，0，0），A（2，0，0），C（0，2，0），C₁（0，2，2），
E（2，2，1），F（0，0，1），B₁（2，2，2），
所以

FC1

=（0，2，1），

DA

=（2，0，0），

AE

=（0，2，1）．
（1）设

n1

=（x₁，y₁，z₁）是平面ADE的法向量，则

n1

⊥

DA

，

n1

⊥

AE

，
即

n1 • DA =2x1 n1 • AE =2y1+z1

⇒

x1=0 z1=-2y1

，令z₁=2⇒y₁=-1，
所以

n1

=（0，-1，2）因为

n1

•

FC1

=-2+2=0，所以

n1

⊥

FC1

，
又因为FC₁?平面ADE，
即FC₁∥平面ADE．
（2）因为

C1B1

=（2，0，0），设

n2

=（x₂，y₂，z₂）是平面B₁C₁F的一个法向量．
由

n2

⊥

FC1

，

n2

⊥

C1B1

，得

n2 • FC1 =2y2+z2=0 n2 • C1B1 =2x2=0

⇒

x2=0 z2=-2y2

．
令z₂=2⇒y₂=-1，所以

n2

=（0，-1，2），
所以

n1

=

n2

，所以平面ADE∥平面B₁C₁F．

点评：本题考查空间几何体的特征，空间向量证明直线与平面平行平面与平面平行的判断方法，考查计算能力．