题目内容
已知sin(
-α)=
,则cos(π-2α)=( )
| π |
| 2 |
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
考点:运用诱导公式化简求值
专题:计算题,三角函数的求值
分析:由已知及诱导公式可求cosα,由诱导公式和二倍角公式化简所求后代入cosα的值即可求解.
解答:
解:∵sin(
-α)=cosα=
,
∴cos(π-2α)=-cos2α=1-2cos2α═1-2×(
)2=
,
故选:A.
| π |
| 2 |
| 3 |
| 5 |
∴cos(π-2α)=-cos2α=1-2cos2α═1-2×(
| 3 |
| 5 |
| 7 |
| 25 |
故选:A.
点评:本题主要考察了诱导公式和二倍角公式的应用,属于基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若cos(π-x)=-
,x∈[0,2π],则x=( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=
的定义域为( )
| 4x |
| A、[0,+∞) |
| B、(0,+∞) |
| C、{0} |
| D、以上答案都不对 |
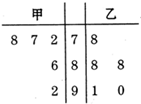 甲、乙两位同学在高二5次月考的数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是
甲、乙两位同学在高二5次月考的数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|