题目内容
已知向量
=（
，sin（x-
）），
=（sin（2x-
），2sin（x-
）），定义函数f（x）=
•
．
（1）求函数f（x）的表达式；
（2）令φ（x）=f（x+
），试画出函数φ（x）在[0，π]这个周期内的图象．
| a |
| 3 |
| π |
| 12 |
| b |
| π |
| 6 |
| π |
| 12 |
| a |
| b |
（1）求函数f（x）的表达式；
（2）令φ（x）=f（x+
| π |
| 4 |
考点：平面向量数量积的运算,五点法作函数y=Asin（ωx+φ）的图象
专题：计算题,三角函数的图像与性质,平面向量及应用
分析：（1）运用向量的数量积的坐标表示和二倍角公式以及两角差的正弦公式，即可化简得到f（x）的解析式；
（2）取五个点，描出它们，再由光滑曲线连接即可得到一个周期的图象．
（2）取五个点，描出它们，再由光滑曲线连接即可得到一个周期的图象．
解答：
解：（1）向量
=（
，sin（x-
）），
=（sin（2x-
），2sin（x-
）），
则f（x）=
•
=
sin（2x-
）+2sin2（x-
）=
sin（2x-
）-cos（2x-
）+1
=2sin（2x-
-
）-1=2sin（2x-
）-1；
（2）φ（x）=f（x+
）=2sin（2x+
）-1，
可分别取（0，0）、（
，
-1）、（
，-2）、（
，-
-1）、（π，0），
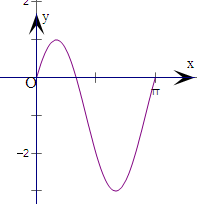
在平面直角坐标系中，描出它们，并用光滑曲线连接，如图．
解：（1）向量| a |
| 3 |
| π |
| 12 |
| b |
| π |
| 6 |
| π |
| 12 |
则f（x）=
| a |
| b |
| 3 |
| π |
| 6 |
| π |
| 12 |
| 3 |
| π |
| 6 |
| π |
| 6 |
=2sin（2x-
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
（2）φ（x）=f（x+
| π |
| 4 |
| π |
| 6 |
可分别取（0，0）、（
| π |
| 4 |
| 3 |
| π |
| 2 |
| 3π |
| 4 |
| 3 |
在平面直角坐标系中，描出它们，并用光滑曲线连接，如图．
点评：本题考查平面向量的数量积的坐标表示，考查三角函数的化简和作图，属于基础题．
练习册系列答案
习题精选系列答案
相关题目
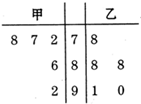甲、乙两位同学在高二5次月考的数学成绩统计如茎叶图所示，若甲、乙两人的平均成绩分别是. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|