题目内容
已知函数f(x)=logn+1x(n>0),且 g(x)=x+f(x+2)-f(n-x)是奇函数.
(1)求实数n的值;
(2)求g(x)图象与直线y=-2,x=1围成的封闭图形的面积S;
(3)对于任意a,b,c∈[M,+∞),且a≥b≥c.当a、b、c能作为一个三角形的三边长时,f(a),f(b),f(c)也总能作为某个三角形的三边长,试求M的最小值.
(1)求实数n的值;
(2)求g(x)图象与直线y=-2,x=1围成的封闭图形的面积S;
(3)对于任意a,b,c∈[M,+∞),且a≥b≥c.当a、b、c能作为一个三角形的三边长时,f(a),f(b),f(c)也总能作为某个三角形的三边长,试求M的最小值.
考点:分析法和综合法,函数图象的作法,函数奇偶性的性质,对数的运算性质
专题:函数的性质及应用
分析:(1)由题意可得g(x)=x+logn+1(
)为奇函数,由f(0)=0,解得n的值.
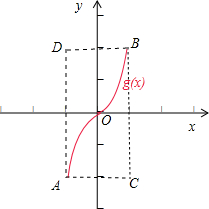
(2)由(1)可得g(x)是增函数,定义域为[-1,1],g(x)图象与直线y=-2,x=1围成的封闭图形为矩形ACBD.再根据g(x)的图象平分矩形ACBD的面积.可得所求的面积为S.
(3)由题意可得b+c>a,f(b)+f(c)>f(a),可得 bc>a.由于log3c>0,得c>1,经过检验,当0<M≤1不满足题意.再根据当1<M<2时,经过检验也不满足题意,可得M的最小值为2.
| x+2 |
| n-x |
(2)由(1)可得g(x)是增函数,定义域为[-1,1],g(x)图象与直线y=-2,x=1围成的封闭图形为矩形ACBD.再根据g(x)的图象平分矩形ACBD的面积.可得所求的面积为S.
(3)由题意可得b+c>a,f(b)+f(c)>f(a),可得 bc>a.由于log3c>0,得c>1,经过检验,当0<M≤1不满足题意.再根据当1<M<2时,经过检验也不满足题意,可得M的最小值为2.
解答:
 解:(1)由题意可得g(x)=x+f(x+2)-f(n-x)
解:(1)由题意可得g(x)=x+f(x+2)-f(n-x)
=x+logn+1(x+2)-logn+1x(n-x)
=x+logn+1(
)为奇函数,
故有f(0)=0+logn+1(
)=0,解得n=2.
(2)由(1)可得g(x)=x+logn+1(x+2)-logn+1x(n-x)
是增函数,定义域为[-1,1],
g(x)图象与直线y=-2,x=1围成的封闭图形为矩形ACBD,
A(-1,-2),B(1,2).
再根据曲线的对称性可得,函数g(x)的图象平分矩形ACBD的面积.
故所求的面积为S=
[(1-(-1)]×4=4.
(3)由题意可得b+c>a,由于f(a),f(b),f(c)能作为某个三角形的三边,
故有f(b)+f(c)>f(a),即log3b+log3c>log3a,即 bc>a.
由于log3c>0,∴c>1,故0<M≤1不满足题意.
再根据当1<M<2时,取b=c=M,a=M2,有M+M>M2,即b+c>a,满足条件;
但此时 log3M+log3M=2log3M=log3M2,即f(b)+f(c)=f(a),
f(a),f(b),f(c)不能作为某个三角形的三边.
综上可得,M的最小值为2.
 解:(1)由题意可得g(x)=x+f(x+2)-f(n-x)
解:(1)由题意可得g(x)=x+f(x+2)-f(n-x)=x+logn+1(x+2)-logn+1x(n-x)
=x+logn+1(
| x+2 |
| n-x |
故有f(0)=0+logn+1(
| 0+2 |
| n-0 |
(2)由(1)可得g(x)=x+logn+1(x+2)-logn+1x(n-x)
是增函数,定义域为[-1,1],
g(x)图象与直线y=-2,x=1围成的封闭图形为矩形ACBD,
A(-1,-2),B(1,2).
再根据曲线的对称性可得,函数g(x)的图象平分矩形ACBD的面积.
故所求的面积为S=
| 1 |
| 2 |
(3)由题意可得b+c>a,由于f(a),f(b),f(c)能作为某个三角形的三边,
故有f(b)+f(c)>f(a),即log3b+log3c>log3a,即 bc>a.
由于log3c>0,∴c>1,故0<M≤1不满足题意.
再根据当1<M<2时,取b=c=M,a=M2,有M+M>M2,即b+c>a,满足条件;
但此时 log3M+log3M=2log3M=log3M2,即f(b)+f(c)=f(a),
f(a),f(b),f(c)不能作为某个三角形的三边.
综上可得,M的最小值为2.
点评:本题主要考查函数的奇偶性的应用,对数的运算性质,体现了数形结合的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
圆(x+2)2+y2=5关于直线x-y+1=0对称的圆的方程为( )
| A、(x-2)2+y2=5 |
| B、x2+(y-2)2=5 |
| C、(x-1)2+(y-1)2=5 |
| D、(x+1)2+(y+1)2=5 |
 某校为了了解学生的营养状况,从该校中随机抽取400名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).由图中数据可知该400名的学生中,身高在120cm到130cm的人数为
某校为了了解学生的营养状况,从该校中随机抽取400名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).由图中数据可知该400名的学生中,身高在120cm到130cm的人数为 若一个三棱柱的底面是正三角形,其正(主)视图如图所示,则它的体积
若一个三棱柱的底面是正三角形,其正(主)视图如图所示,则它的体积