题目内容
 在三棱柱ABC-A1B1C1中,直线AA1与底面ABC所成的角是直角,直线AB与B1C1所成的角为45°,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、A1C、BC的中点.
在三棱柱ABC-A1B1C1中,直线AA1与底面ABC所成的角是直角,直线AB与B1C1所成的角为45°,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、A1C、BC的中点.(1)求证:DE∥平面ABC;
(2)求证:平面AB1F⊥平面AEF.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(1)取AB中点G,连结DG,GC,连接A1B、A1E,并延长A1E交AC的延长线于点P,连接BP,证明DE∥BP,即可证明DE∥平面ABC;
(2)证明B1F⊥平面AEF,即可证明平面AB1F⊥平面AEF.
(2)证明B1F⊥平面AEF,即可证明平面AB1F⊥平面AEF.
解答:
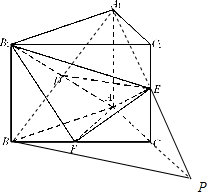 证明:(1)取AB中点G,连结DG,GC.
证明:(1)取AB中点G,连结DG,GC.
连接A1B、A1E,并延长A1E交AC的延长线于点P,连接BP.
由E为C1C的中点,A1C1∥CP,
由题意A1E=EP,
∵D、E是A1B、A1P的中点,∴DE∥BP,
又∵BP?平面ABC,DE?平面ABC,∴DE∥平面ABC┉┉(7分)
(2)∵△ABC为等腰直角三角形,F为BC的中点,
∴BC⊥AF,
又∵直线AA1与底面ABC所成的角为直角
∴B1B⊥平面ABC,B1F⊥AF,
设AB=AA1=2,则B1F=
,EF=
,B1E=3
∴B1F⊥EF,∴B1F⊥平面AEF;
∴平面AB1F⊥平面AEF.┉┉(14分)
 证明:(1)取AB中点G,连结DG,GC.
证明:(1)取AB中点G,连结DG,GC.连接A1B、A1E,并延长A1E交AC的延长线于点P,连接BP.
由E为C1C的中点,A1C1∥CP,
由题意A1E=EP,
∵D、E是A1B、A1P的中点,∴DE∥BP,
又∵BP?平面ABC,DE?平面ABC,∴DE∥平面ABC┉┉(7分)
(2)∵△ABC为等腰直角三角形,F为BC的中点,
∴BC⊥AF,
又∵直线AA1与底面ABC所成的角为直角
∴B1B⊥平面ABC,B1F⊥AF,
设AB=AA1=2,则B1F=
| 6 |
| 3 |
∴B1F⊥EF,∴B1F⊥平面AEF;
∴平面AB1F⊥平面AEF.┉┉(14分)
点评:本题考查直线与平面平行的判定,考查平面与平面垂直的判定,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
已知正方体ABCD-A1B1C1D1的掕长为2,动点P在正方体表面运动,且PA=r,(0<r<2
),记P的轨迹长度为f(r),则关于r的方程f(r)=k的解的个数可以为( )
| 3 |
| A、0,2,3,4 |
| B、0,1,2 |
| C、1,2,3 |
| D、0,2,4,6 |