题目内容
已知直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=4，DC=6，BC=2．（1）若P是腰DC的中点，求|
| PA |
| PB |
（2）在腰DC上是否存在点P，使∠APB=90°．若存在，求出点P的位置；若不存在，请说明理由．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（1）如图所示，A（4，0），B（2，6），C（0，6），P（0，3），
利用向量的坐标运算即可得出
+3
．
（2）设点P（0，t）（0≤t≤6）．利用
•
=0，解得t即可．
利用向量的坐标运算即可得出
| PA |
| PB |
（2）设点P（0，t）（0≤t≤6）．利用
| PA |
| PB |
解答：
解：（1）如图所示，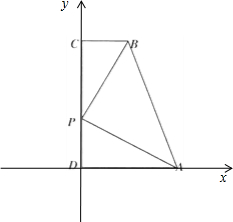
A（4，0），B（2，6），C（0，6），P（0，3），
则
+3
=（4，-3）+3（2，3）=（10，6）．
∴|
+3
|=
=2
．
（2）设
点P（0，t）（0≤t≤6）．则
•
=（4，-t）•（2，6-t）=8-6t+t2=0，解得t=2或4．∴存在点P，使∠APB=90°，点P为CD的两个三等分点．
A（4，0），B（2，6），C（0，6），P（0，3），
则
| PA |
| PB |
∴|
| PA |
| PB |
| 102+62 |
| 34 |
（2）设
点P（0，t）（0≤t≤6）．则
| PA |
| PB |
点评：本题考查了向量的坐标运算、向量垂直与数量积的关系，考查了计算能力，属于中档题．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
设直线l经过点（0，-2），且与圆x2+y2=1相切，则l的斜率是（ ）
| A、±1 | ||||
B、±
| ||||
C、±
| ||||
D、±
|