题目内容
已知
=(3sinx,
),
=(cosx,cos2x-
),函数f(x)=
•
,
(1)求函数f(x)的周期;
(2)写出函数f(x)的递减区间;
(3)求f(x)在[0,
]上的最值并求出相应的x的值.
| a |
| 3 |
| b |
| 1 |
| 2 |
| a |
| b |
(1)求函数f(x)的周期;
(2)写出函数f(x)的递减区间;
(3)求f(x)在[0,
| π |
| 2 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用数量积运算、倍角公式、两角和差的正弦公式可得:函数f(x)=
•
=
sin(2x+
).
(1)利用T=
即可得出周期;
(2)利用正弦函数的单调性即可得出.
(3)利用已知区间及其正弦函数的单调性即可得出.
| a |
| b |
| 3 |
| π |
| 6 |
(1)利用T=
| 2π |
| ω |
(2)利用正弦函数的单调性即可得出.
(3)利用已知区间及其正弦函数的单调性即可得出.
解答:
解:函数f(x)=
•
=3sinxcosx+
(cos2x-
)
=
sin2x+
cos2x=
sin(2x+
).
(1)T=
=
=π.
(2)由
+2kπ≤2x+
≤
+2kπ,k∈Z,
解得:
+kπ≤x≤
+kπ,k∈Z,
∴函数f(x)的减区间为[
+kπ,
+kπ],k∈Z.
(3)由0≤x≤
得,
≤2x+
≤
∴当2x+
=
,x=
时,f(x)min=-
,
当2x+
=
,x=
时,f(x)max=
.
| a |
| b |
=3sinxcosx+
| 3 |
| 1 |
| 2 |
=
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 6 |
(1)T=
| 2π |
| ω |
| 2π |
| 2 |
(2)由
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
解得:
| π |
| 6 |
| 2π |
| 3 |
∴函数f(x)的减区间为[
| π |
| 6 |
| 2π |
| 3 |
(3)由0≤x≤
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴当2x+
| π |
| 6 |
| 7π |
| 6 |
| π |
| 2 |
| ||
| 2 |
当2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| 3 |
点评:本题考查了数量积运算、倍角公式、两角和差的正弦公式、正弦函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=4,DC=6,BC=2.
已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=4,DC=6,BC=2.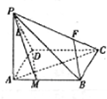 如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA⊥平面ABCD,AB=
如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA⊥平面ABCD,AB=