题目内容
已知(2
+
)n的展开式中,第5项的二项式系数与第3项的二项式系数之比是7:2.
(Ⅰ)求展开式中含x
项的系数;
(Ⅱ)求展开式中系数最大的项.
| x |
| 3 | x2 |
(Ⅰ)求展开式中含x
| 11 |
| 2 |
(Ⅱ)求展开式中系数最大的项.
考点:二项式系数的性质
专题:计算题,二项式定理
分析:(Ⅰ)由第5项的二项式系数与第3项的二项式系数之比是7:2,求出n,再求展开式中含x项的系数;
(Ⅱ)设第r+1项的系数最大,则有
,即可求展开式中系数最大的项.
(Ⅱ)设第r+1项的系数最大,则有
|
解答:
解:(Ⅰ)由题意知
=
,整理得42=(n-2)(n-3),解得n=9…(2分)
∴通项公式为Tr+1=
•29-rx
…(4分)
令
=
,解得r=6.
∴展开式中含x
项的系数为
•29-6=672.…(6分)
(Ⅱ)设第r+1项的系数最大,则有
…(8分)
∴
,
∵r∈N且0≤r≤9,∴r=3.…(10分)
∴展开式中系数最大的项为T4=
•26x5=5376x5.…(12分)
| ||
|
| 7 |
| 2 |
∴通项公式为Tr+1=
| C | r 9 |
| 27+r |
| 6 |
令
| 27+r |
| 6 |
| 11 |
| 2 |
∴展开式中含x
| 11 |
| 2 |
| C | 6 9 |
(Ⅱ)设第r+1项的系数最大,则有
|
∴
|
∵r∈N且0≤r≤9,∴r=3.…(10分)
∴展开式中系数最大的项为T4=
| C | 3 9 |
点评:本题考查二项展开式中二项式系数与系数和展开式中最大的项问题,难度较大,易出错.要正确区分这两个概念.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
函数y=log
(2x-x2)的单调递增区间为( )
| 1 |
| 2 |
| A、[1,+∞) |
| B、(-∞,1] |
| C、[1,2) |
| D、(0,1] |
 已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=4,DC=6,BC=2.
已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=4,DC=6,BC=2.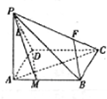 如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA⊥平面ABCD,AB=
如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA⊥平面ABCD,AB=