题目内容
函数f(x)=ln|x-2|-m(m∈R)的所有零点之和为( )
| A、-4 | B、2 |
| C、4 | D、与实数m有关 |
考点:函数的零点
专题:计算题,函数的性质及应用
分析:函数f(x)=ln|x-2|-m(m∈R)的零点即方程ln|x-2|=m的解,从而求解.
解答:
解:函数f(x)=ln|x-2|-m(m∈R)的零点即方程ln|x-2|=m的解,
即|x-2|=em;
故x=em+2或x=-em+2;
故函数f(x)=ln|x-2|-m(m∈R)的所有零点之和为em+2-em+2=4;
故选C.
即|x-2|=em;
故x=em+2或x=-em+2;
故函数f(x)=ln|x-2|-m(m∈R)的所有零点之和为em+2-em+2=4;
故选C.
点评:本题考查了函数的零点与方程的根的关系应用,属于基础题.

练习册系列答案
相关题目
用二分法求函数f(x)=3x-x-4的一个零点,其参考数据如下:
据此数据,可得f(x)的一个零点的近似值(精确到0.01)为( )
| f(1.6)=0.200 | f(1.5875)=0.133 | f(1.5750)=0.067 |
| f(1.5625)=0.003 | f(1.5562)=-0.029 | f(1.550)=-0.060 |
| A、1.58 | B、1.57 |
| C、1.56 | D、1.55 |
若一个圆柱的侧面展开图是一个正方形,则这个圆柱的全面积与侧面积的比是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 一个几何体的三视图如图所示,其中俯视图与侧视图均为半径是2的圆,则这个几何体的表面积是( )
一个几何体的三视图如图所示,其中俯视图与侧视图均为半径是2的圆,则这个几何体的表面积是( )| A、16π | B、14π |
| C、12π | D、8π |
双曲线C:
-
=1(a>0,b>0)的左右焦点分别为F1、F2,离心率为
,过F1且与x轴垂直的直线与双曲线C交于A,B两点,则|AF1|与|AF2|的关系是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| A、2|AF2|=3|AF1| |
| B、|AF2|=2|AF1| |
| C、|AF2|=3|AF1| |
| D、3|AF2|=4|AF1| |
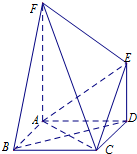 如图所示的几何体中,直线AF⊥平面ABCD,且ABCD为正方形,ADEF为梯形,DE∥AF,又AB=1,AF=2DE=2a.
如图所示的几何体中,直线AF⊥平面ABCD,且ABCD为正方形,ADEF为梯形,DE∥AF,又AB=1,AF=2DE=2a.