题目内容
13.设函数$f(x)=4cos(x-\frac{π}{6})sinx-2cos(2x+π)$,则函数f(x)的最大值和最小值分别为( )| A. | 13和-11 | B. | 8和-6 | C. | 1和-3 | D. | 3和-1 |
分析 利用辅助角公式诱导公式和两角和余差的基本公式将函数化为y=Asin(ωx+φ)的形式,利用三角函数的有界限求最大值和最小值.
解答 解:函数$f(x)=4cos(x-\frac{π}{6})sinx-2cos(2x+π)$=4×cos$\frac{π}{6}$sinxcox+4×sin$\frac{π}{6}$sin2x+2cos2x
=$\sqrt{3}$sin2x+1-cos2x+2cos2x=$\sqrt{3}$sin2x+cos2x+1=2sin(2x+$\frac{π}{6}$)+1.
∵-1≤sin(2x+$\frac{π}{6}$)≤1
∴-1≤f(x)≤3.
故函数f(x)的最大值和最小值分别:3:和-1.
故选:D.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于基础题.

练习册系列答案
相关题目
4.已知F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的两个焦点,PQ是经过F1且垂直于x轴的双曲线的弦,若∠PF2Q=90°,则双曲线的离心率为( )
| A. | 2 | B. | $2\sqrt{2}$ | C. | $\sqrt{2}-1$ | D. | $1+\sqrt{2}$ |
1.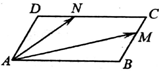 如图,在平行四边形ABCD中,$∠BAD=\frac{π}{3}$,AB=2,AD=1,若M、N分别是边BC、CD上的点,且满足$\frac{BM}{BC}=\frac{NC}{DC}=λ$,其中λ∈[0,1],则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是( )
如图,在平行四边形ABCD中,$∠BAD=\frac{π}{3}$,AB=2,AD=1,若M、N分别是边BC、CD上的点,且满足$\frac{BM}{BC}=\frac{NC}{DC}=λ$,其中λ∈[0,1],则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是( )
 如图,在平行四边形ABCD中,$∠BAD=\frac{π}{3}$,AB=2,AD=1,若M、N分别是边BC、CD上的点,且满足$\frac{BM}{BC}=\frac{NC}{DC}=λ$,其中λ∈[0,1],则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是( )
如图,在平行四边形ABCD中,$∠BAD=\frac{π}{3}$,AB=2,AD=1,若M、N分别是边BC、CD上的点,且满足$\frac{BM}{BC}=\frac{NC}{DC}=λ$,其中λ∈[0,1],则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是( )| A. | [0,3] | B. | [1,4] | C. | [2,5] | D. | [1,7] |
8.设集合A={x|x2-x-6<0},B={x|-3≤x≤1},则A∪B等于( )
| A. | [-2,1) | B. | (-2,1] | C. | [-3,3) | D. | (-3,3] |
18.某单位生产A、B两种产品,需要资金和场地,生产每吨A种产品和生产每吨B种产品所需资金和场地的数据如表所示:
现有资金12万元,场地400平方米,生产每吨A种产品可获利润3万元;生产每吨B种产品可获利润2万元,分别用x,y表示计划生产A、B两种产品的吨数.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问A、B两种产品应各生产多少吨,才能产生最大的利润?并求出此最大利润.
| 资源 产品 | 资金(万元) | 场地(平方米) |
| A | 2 | 100 |
| B | 35 | 50 |
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问A、B两种产品应各生产多少吨,才能产生最大的利润?并求出此最大利润.
5.已知圆锥的底面半径为1,侧面展开图的圆心角为60°,则此圆锥的表面积为( )
| A. | 3π | B. | 5π | C. | 7π | D. | 9π |
14.方程xy2+x2y=1所表示的曲线( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于直线y=x对称 |
15.已知函数y=f(x)的图象关于直线x=-1对称,且当x∈(0,+∞)时,有f(x)=$\frac{1}{x}$,当x∈(-∞,-2)时,f(x)的解析式为( )
| A. | f(x)=-$\frac{1}{x}$ | B. | f(x)=-$\frac{1}{x-2}$ | C. | f(x)=$\frac{1}{x+2}$ | D. | f(x)=-$\frac{1}{x+2}$ |