题目内容
4.已知F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的两个焦点,PQ是经过F1且垂直于x轴的双曲线的弦,若∠PF2Q=90°,则双曲线的离心率为( )| A. | 2 | B. | $2\sqrt{2}$ | C. | $\sqrt{2}-1$ | D. | $1+\sqrt{2}$ |
分析 根据PQ是经过F1且垂直于x轴的双曲线的弦,∠PF2Q=90°,可得|PF1|=|F1F2|,从而可得e的方程,即可求得双曲线的离心率.
解答 解:∵PQ是经过F1且垂直于x轴的双曲线的弦,∠PF2Q=90°,
∴|PF1|=|F1F2|
∴$\frac{{b}^{2}}{a}$=2c,
∴e2-2e-1=0,
∵e>1,
∴e=1+$\sqrt{2}$.
故选:D.
点评 本题考查双曲线的离心率,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
15.下列选项中,存在实数m使得定义域和值域都是(m,+∞)的函数是( )
| A. | y=ex | B. | y=lnx | C. | y=x2 | D. | y=$\frac{x-1}{x+1}$ |
19.“m>n>0”是“方程mx2+ny2=1表示焦点在y轴上的椭圆”的( )
| A. | 充而分不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
16.设变量x,y满足约束条件$\left\{\begin{array}{l}x-y+1≥0\\ x+y-1≥0\\ 3x-y-3≤0\end{array}\right.$则目标函数z=4x+y的最大值为( )
| A. | 4 | B. | 11 | C. | 12 | D. | 14 |
13.设函数$f(x)=4cos(x-\frac{π}{6})sinx-2cos(2x+π)$,则函数f(x)的最大值和最小值分别为( )
| A. | 13和-11 | B. | 8和-6 | C. | 1和-3 | D. | 3和-1 |
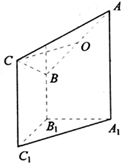 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知∠A1B1C1=90°,AA1=4,BB1=2,CC1=3,A1B1=B1C1=1.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知∠A1B1C1=90°,AA1=4,BB1=2,CC1=3,A1B1=B1C1=1.