Question

14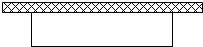．某农场计划使用可以做出30米栅栏的材料，在靠墙（墙足够长）的位置围出一块矩形的菜园（如图）．
问：（1）要是菜园的面积不小于100平方米，试确定与墙平行栅栏的长度范围；
（2）与墙平行栅栏的长为多少时围成的菜园面积最大？最大面积为多少？

Answer 1

分析 （1）设与墙平行栅栏的长度为x，则矩形的另一条边长为$\frac{30-x}{2}$，从而解不等式x•$\frac{30-x}{2}$≥100即可；
（2）S=x•$\frac{30-x}{2}$≤$\frac{1}{2}$（$\frac{x+30-x}{2}$）²=$\frac{225}{2}$，从而确定最值．

解答 解：（1）设与墙平行栅栏的长度为x，则矩形的另一条边长为$\frac{30-x}{2}$，
故S=x•$\frac{30-x}{2}$≥100，
解得，10≤x≤20，
故与墙平行栅栏的长度为10～20m；
（2）S=x•$\frac{30-x}{2}$≤$\frac{1}{2}$（$\frac{x+30-x}{2}$）²=$\frac{225}{2}$，
（当且仅当x=15时，等号成立）；
故与墙平行栅栏的长为15m时围成的菜园面积最大，
最大面积为$\frac{225}{2}$m²．

点评 本题考查了基本不等式在求最值时的应用，同时考查了二次不等式的解法．