题目内容
5.已知函数f(x)=|ax-3|(a>0),g(x)=|x+$\frac{5}{2}$|.(1)若不等式f(x)-5≤0的解集为[-1,4],求不等式f(x)+g(x)≤$\frac{11}{2}$的解集;
(2)在(1)的条件下,若存在实数x,使得对任意的正数a,b,m满足$\frac{b}{a}$+$\frac{am}{b}$≥f(x)+g(x)成立,求实数m的最小值.
分析 (1)利用f(x)-5≤0的解集为[-1,4],求出a,分类讨论求不等式f(x)+g(x)≤$\frac{11}{2}$的解集;
(2)在(1)的条件下,若存在实数x,使得对任意的正数a,b,m满足$\frac{b}{a}$+$\frac{am}{b}$≥f(x)+g(x)成立,则$\frac{b}{a}$+$\frac{am}{b}$≥[f(x)+g(x)]min,即可求实数m的最小值.
解答 解:(1)∵f(x)-5≤0的解集为[-1,4],
∴|ax-3|≤5的解集为[-1,4],
∴$\left\{\begin{array}{l}{|-a-3|=5}\\{|4a-3|=5}\end{array}\right.$,
∵a>0,∴a=2,
∴f(x)=|2x-3|,
∴|2x-3|+|x+$\frac{5}{2}$|≤$\frac{11}{2}$
x<-$\frac{5}{2}$,3-2x-x-$\frac{5}{2}$≤$\frac{11}{2}$,∴x≥-$\frac{5}{3}$,∴x∈∅,
-$\frac{5}{2}$≤x≤$\frac{3}{2}$,3-2x+x+$\frac{5}{2}$≤$\frac{11}{2}$,∴x≥0,∴0≤x≤$\frac{3}{2}$,
x>$\frac{3}{2}$,2x-3+x+$\frac{5}{2}$≤$\frac{11}{2}$,∴x≤2,∴$\frac{3}{2}$<x≤2,
∴0≤x≤2,
∴不等式f(x)+g(x)≤$\frac{11}{2}$的解集为{x|0≤x≤2};
(2)∵存在实数x,使得对任意的正数a,b,m满足$\frac{b}{a}$+$\frac{am}{b}$≥f(x)+g(x)成立,
∴$\frac{b}{a}$+$\frac{am}{b}$≥0
又$\frac{b}{a}$+$\frac{am}{b}$≥2$\sqrt{m}$,
∴2$\sqrt{m}$≥0
∴m≥0,
∴实数m的最小值是0.
点评 本题考查不等式的解法,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案| A. | a≤1 | B. | a≤-1 | C. | a≥1 | D. | a≥-1 |
| A. | 72种 | B. | 36种 | C. | 144种 | D. | 108种 |
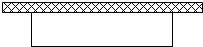 某农场计划使用可以做出30米栅栏的材料,在靠墙(墙足够长)的位置围出一块矩形的菜园(如图).
某农场计划使用可以做出30米栅栏的材料,在靠墙(墙足够长)的位置围出一块矩形的菜园(如图).