题目内容
2.若△ABC满足a2-b2+c2-ac=0,则∠B=60°.分析 根据题意,由a2-b2+c2-ac=0可得a2+c2-b2=ac,将其代入余弦定理cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$中,可得cosB=$\frac{1}{2}$,进而可得B的值,即可得答案.
解答 解:根据题意,a2-b2+c2-ac=0,则a2+c2-b2=ac,
则cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{ac}{2ac}$=$\frac{1}{2}$,
则∠B=60°;
故答案为:60°.
点评 本题考查余弦定理的运用,关键是牢记余弦定理的公式.

练习册系列答案
相关题目
13.若不等式组$\left\{\begin{array}{l}x-y+2≥0\\ x-5y+10≤0\\ x+y-8≤0\end{array}\right.$所表示的平面区域存在点(x0,y0)使ax0+y0+2≤0成立,则实数a的取值范围是( )
| A. | a≤1 | B. | a≤-1 | C. | a≥1 | D. | a≥-1 |
10.在屠哟哟获得2015年诺贝尔生理学或医学奖后,某市在两所学铰之间举办了学习交流会,两所学饺各选派3名学生代表,校际间轮流发言,那么不同的发言顺序共有( )
| A. | 72种 | B. | 36种 | C. | 144种 | D. | 108种 |
7.在等比数列{an}中,已知a1=1,q=2,则第5项至第10项的和为( )
| A. | 63 | B. | 992 | C. | 1008 | D. | 1023 |
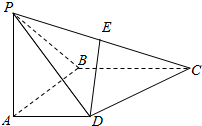 如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,且∠PAB=∠ABC=90°,AD∥BC,PA=AB=BC=2AD,E是PC的中点.
如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,且∠PAB=∠ABC=90°,AD∥BC,PA=AB=BC=2AD,E是PC的中点.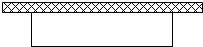 某农场计划使用可以做出30米栅栏的材料,在靠墙(墙足够长)的位置围出一块矩形的菜园(如图).
某农场计划使用可以做出30米栅栏的材料,在靠墙(墙足够长)的位置围出一块矩形的菜园(如图).