题目内容
6.f(x)=x(x+1)(x+2)…(x+n),则f′(0)=( )| A. | 0 | B. | 1 | C. | n | D. | n! |
分析 由导数的乘法法则求导数,把x=0代入计算可得.
解答 解:令g(x)=(x+1)(x+2)•…•(x+n),
∵f(x)=xg(x),
∴f′(x)=g(x)+xg′(x),
∵g(0)=1×2×3×…×n=n!
∴f′(0)=g(0)+0×g′(0)=n!
故选:D.
点评 此题考查学生灵活运用求导法则化简求值,会根据自变量的值求出相应导函数的值,是一道中档题

练习册系列答案
相关题目
18.已知数列{an}前n项和为Sn=n2-2n+a(a∈R,n∈N*),若该数列是等差数列则a的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 不确定 |
16.已知函数f(x)=loga[($\frac{1}{a}$-1)x+3]在区间[2,3]上的函数值小于1恒成立,则实数a的取值范围是( )
| A. | (0,1)∪(2,+∞) | B. | (0,1) | C. | (2,+∞) | D. | (1,+∞) |
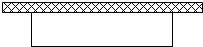 某农场计划使用可以做出30米栅栏的材料,在靠墙(墙足够长)的位置围出一块矩形的菜园(如图).
某农场计划使用可以做出30米栅栏的材料,在靠墙(墙足够长)的位置围出一块矩形的菜园(如图).