题目内容
19.已知函数f(x)=x2+ax+3-a,若x∈[-2,2]的函数值大于0恒成立,求实数a的取值范围.分析 根据对称轴与[-2,2]的关系判断f(x)的单调性,利用单调性求出fmin(x),令fmin(x)>0得出a的范围.
解答 解:f(x)的图象开口向上,对称轴为x=-$\frac{a}{2}$.
(1)若-$\frac{a}{2}$≤-2,即a≥4时,f(x)在[-2,2]上是增函数,∴fmin(x)=f(-2)=7-3a,
令fmin(x)>0,即7-3a>0,解得a<$\frac{7}{3}$(舍).
(2)若-$\frac{a}{2}$≥2,即a≤-4时,f(x)在[-2,2]上是减函数,∴fmin(x)=f(2)=7+a.
令fmin(x)>0,即7+a>0,解得a>-7,∴-7<a≤-4.
(3)若-2<-$\frac{a}{2}$<2,即-4<a<4时,f(x)在[-2,-$\frac{a}{2}$]上是减函数,在(-$\frac{a}{2}$,2]上是增函数,∴fmin(x)=f(-$\frac{a}{2}$)=-$\frac{{a}^{2}}{4}$-a+3.
令fmin(x)>0,即-$\frac{{a}^{2}}{4}$-a+3>0,解得-6<a<2,∴-4<a<2.
综上,实数a的取值范围是(-7,2).
点评 本题考查了二次函数的单调性与最值,需要讨论对称轴与区间的关系,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.在屠哟哟获得2015年诺贝尔生理学或医学奖后,某市在两所学铰之间举办了学习交流会,两所学饺各选派3名学生代表,校际间轮流发言,那么不同的发言顺序共有( )
| A. | 72种 | B. | 36种 | C. | 144种 | D. | 108种 |
7.在等比数列{an}中,已知a1=1,q=2,则第5项至第10项的和为( )
| A. | 63 | B. | 992 | C. | 1008 | D. | 1023 |
9.函数f(x)=log0.5$\frac{2-x}{2+x}$是( )
| A. | 既是奇函数又是偶函数 | B. | 奇函数 | ||
| C. | 既不是奇函数也不是偶函数 | D. | 偶函数 |
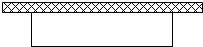 某农场计划使用可以做出30米栅栏的材料,在靠墙(墙足够长)的位置围出一块矩形的菜园(如图).
某农场计划使用可以做出30米栅栏的材料,在靠墙(墙足够长)的位置围出一块矩形的菜园(如图).