题目内容
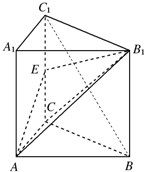
 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,AC=1,AA1=BC=2.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,AC=1,AA1=BC=2.(1)求证:BC1⊥平面AB1C;
(2)求三棱锥C-AB1E的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)根据三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°得出BC⊥AC,AC⊥CC1,即证AC⊥BC1,BC⊥BC1,得证BC1⊥平面AB1C;
(2)转化V C-AB1E=V B1-AEC求解即可.
(2)转化V C-AB1E=V B1-AEC求解即可.
解答:
 (1)证明:∵三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°
(1)证明:∵三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°
∴BC⊥AC,AC⊥CC1,CC1⊥BC,
∴AC⊥面B1BCC1,
∵BC1?平面B1BCC1,
∴AC⊥BC1,
∵AA1=BC=2.
∴BC⊥BC1,
∵AC∩B1C=C,
∴BC1⊥平面AB1C;
(2)∵BB1∥平面A1ACC1,
∴B,B1到平面A1ACC1的距离相等,
∵BC⊥AC,BC⊥CC1,
∴BC⊥平面A1ACC1,
∴V C-AB1E=V B1-AEC=
×
×AC×EC×h=
×
×1×1×2=
,
 (1)证明:∵三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°
(1)证明:∵三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°∴BC⊥AC,AC⊥CC1,CC1⊥BC,
∴AC⊥面B1BCC1,
∵BC1?平面B1BCC1,
∴AC⊥BC1,
∵AA1=BC=2.
∴BC⊥BC1,
∵AC∩B1C=C,
∴BC1⊥平面AB1C;
(2)∵BB1∥平面A1ACC1,
∴B,B1到平面A1ACC1的距离相等,
∵BC⊥AC,BC⊥CC1,
∴BC⊥平面A1ACC1,
∴V C-AB1E=V B1-AEC=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
点评:本题综合考查了直线,平面的垂直与转化,体积求解,属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
已知函数f(x)的定义域为R,且对任意x∈R都有f(x)=f(x-1)+f(x+1),若f(-1)=2,f(1)=3则f(2012)+f(-2012)=( )
| A、-5 | B、-10 |
| C、5055 | D、5060 |
 如图,在一个边长为2的正方形中随机撒入200粒的豆子,恰有120粒落在阴影区域里,则该阴影部分的面积约为( )
如图,在一个边长为2的正方形中随机撒入200粒的豆子,恰有120粒落在阴影区域里,则该阴影部分的面积约为( )A、
| ||
B、
| ||
C、
| ||
D、
|
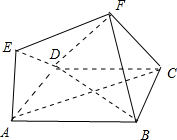 如图所示,已知在多面体ABCDEF中,底面是正方形,EA⊥平面ABCD,EF∥AC且AC=2EF,AB=2AE=2
如图所示,已知在多面体ABCDEF中,底面是正方形,EA⊥平面ABCD,EF∥AC且AC=2EF,AB=2AE=2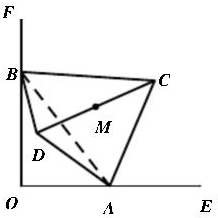 如图,一个棱长为2的正四面体ABCD的两个顶点A,B分别在一个直角(∠EOF)的两边OE,OF上运动,M是棱CD的中点,设点M与O点的距离为d,则d的取值范围是
如图,一个棱长为2的正四面体ABCD的两个顶点A,B分别在一个直角(∠EOF)的两边OE,OF上运动,M是棱CD的中点,设点M与O点的距离为d,则d的取值范围是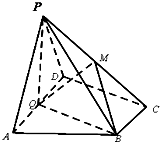 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=