题目内容
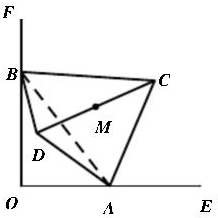如图，一个棱长为2的正四面体ABCD的两个顶点A，B分别在一个直角（∠EOF）的两边OE，OF上运动，M是棱CD的中点，设点M与O点的距离为d，则d的取值范围是考点：点、线、面间的距离计算
专题：空间位置关系与距离
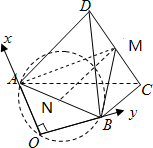
分析：固定正四面体ABCD的位置，则原点O在以AB为直径的球面上运动，所以原点O到直线CD的最近距离为点M到直线CD的距离减去球M的半径，求解即可．
解答：
解：如图，若固定正四面体ABCD的位置，则原点O在以AB为直径的球面上运动，
设AB中点为N，则原点到直线CD的最近距离d等于点N到直线CD的距离减去球N的半径r=
=1，
MB=
，NB=1，所以根据勾股定理得出：MN=
=
，
所求距离的最小值为：d小=
-1．
所求距离的最大值为d大=
+1
故答案为：[
-1，
+1]．
设AB中点为N，则原点到直线CD的最近距离d等于点N到直线CD的距离减去球N的半径r=
| AB |
| 2 |
MB=
| 3 |
| 3-1 |
| 2 |
所求距离的最小值为：d小=
| 2 |
所求距离的最大值为d大=
| 2 |
故答案为：[
| 2 |
| 2 |
点评：本题考查空间想象能力，转化思想的应用，考查分析问题解决问题的能力与计算能力，构造空间几何体，运用几何体之间的关系求解．
练习册系列答案
相关题目
已知集合A={x|-x2+2x＜0}，B={y|y=2x}，R是实数集，则（∁RB）∩A等于（ ）
| A、[0，1] |
| B、（-∞，0） |
| C、（-∞，0] |
| D、（0，1] |
如图是函数与y=2sin（ωx+φ）（ω＞0，|φ|＜
）的图象，那么（ ）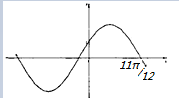
| π |
| 2 |
A、ω=2，φ=-
| ||||
B、ω=2，φ=
| ||||
C、φ=
| ||||
D、ω=
|
已知O是坐标原点，A，B是直线l：x-y+t=0与圆C：x2+y2=4的两个不同交点，若|
|≤|
+
|，则实数t的取值范围是（ ）
| AB |
| OA |
| OB |
A、（-2
| ||||
B、[2，2
| ||||
C、（-2
| ||||
D、[-2
|
如图，三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC，∠ACB=90°，E是棱CC1的中点，AC=1，AA1=BC=2．
如图，正方形ADEF与梯形ABCD所在平面互相垂直，AD⊥CD，AB∥CD，AB=AD=