题目内容
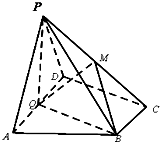 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=| 1 |
| 2 |
| 3 |
(Ⅰ) 求证:平面PQB⊥平面PAD;
(Ⅱ)若二面角M-BQ-C为30°,设PM=tMC,试确定t的值.
考点:二面角的平面角及求法,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)法一:由AD∥BC,BC=
AD,Q为AD的中点,知四边形BCDQ为平行四边形,故CD∥BQ.由∠ADC=90°,知QB⊥AD.由平面PAD⊥平面ABCD,知BQ⊥平面PAD.由此能够证明平面PQB⊥平面PAD.
法二:由AD∥BC,BC=
AD,Q为AD的中点,知四边形BCDQ为平行四边形,故CD∥BQ.由∠ADC=90°,知∠AQB=90°.由PA=PD,知PQ⊥AD,故AD⊥平面PBQ.由此证明平面PQB⊥平面PAD.
(Ⅱ)由PA=PD,Q为AD的中点,知PQ⊥AD.由平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,知PQ⊥平面ABCD.以Q为原点建立空间直角坐标系,利用向量法能够求出t=3.
| 1 |
| 2 |
法二:由AD∥BC,BC=
| 1 |
| 2 |
(Ⅱ)由PA=PD,Q为AD的中点,知PQ⊥AD.由平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,知PQ⊥平面ABCD.以Q为原点建立空间直角坐标系,利用向量法能够求出t=3.
解答:
(Ⅰ)证法一:∵AD∥BC,BC=
AD,Q为AD的中点,
∴四边形BCDQ为平行四边形,∴CD∥BQ.
∵∠ADC=90°∴∠AQB=90°,即QB⊥AD.
又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.
∵BQ?平面PQB,∴平面PQB⊥平面PAD. …(9分)
证法二:AD∥BC,BC=
AD,Q为AD的中点,
∴四边形BCDQ为平行四边形,∴CD∥BQ.
∵∠ADC=90°∴∠AQB=90°.
∵PA=PD,∴PQ⊥AD.
∵PQ∩BQ=Q,∴AD⊥平面PBQ.
∵AD?平面PAD,∴平面PQB⊥平面PAD.…(9分)

解:(Ⅱ)∵PA=PD,Q为AD的中点,∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系.
则平面BQC的法向量为
=(0,0,1);
Q(0,0,0),P(0,0,
),B(0,
,0),C(-1,
,0).
设M(x,y,z),则
=(x,y,z-
),
=(-1-x,
-y,-z),
∵
=t
,
∴
,
∴
…(12分)
在平面MBQ中,
=(0,
,0),
=(-
,
,
),
∴平面MBQ法向量为
=(
,0,t).…(13分)
∵二面角M-BQ-C为30°,
∴cos30°=
=
=
,
∴t=3.…(15分)
| 1 |
| 2 |
∴四边形BCDQ为平行四边形,∴CD∥BQ.
∵∠ADC=90°∴∠AQB=90°,即QB⊥AD.
又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.
∵BQ?平面PQB,∴平面PQB⊥平面PAD. …(9分)
证法二:AD∥BC,BC=
| 1 |
| 2 |
∴四边形BCDQ为平行四边形,∴CD∥BQ.
∵∠ADC=90°∴∠AQB=90°.
∵PA=PD,∴PQ⊥AD.
∵PQ∩BQ=Q,∴AD⊥平面PBQ.
∵AD?平面PAD,∴平面PQB⊥平面PAD.…(9分)

解:(Ⅱ)∵PA=PD,Q为AD的中点,∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系.
则平面BQC的法向量为
| n |
Q(0,0,0),P(0,0,
| 3 |
| 3 |
| 3 |
设M(x,y,z),则
| PM |
| 3 |
| MC |
| 3 |
∵
| PM |
| MC |
∴
|
∴
|
在平面MBQ中,
| QB |
| 3 |
| QM |
| t |
| 1+t |
| ||
| 1+t |
| ||
| 1+t |
∴平面MBQ法向量为
| m |
| 3 |
∵二面角M-BQ-C为30°,
∴cos30°=
|
| ||||
|
|
| t | ||
|
| ||
| 2 |
∴t=3.…(15分)
点评:本题考查平面与平面垂直的证明,求实数的取值.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意合理地进行等价转化,合理地运用向量法进行解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列命题:
(1)5>4;
(2)命题:若a>b,则a+c>b+c的否命题;
(3)“若m>0,则x2+x-m=0有实数根”的逆否命题;
(4)命题:“矩形的两条对角线相等”的逆命题.
其中假命题的个数为( )
(1)5>4;
(2)命题:若a>b,则a+c>b+c的否命题;
(3)“若m>0,则x2+x-m=0有实数根”的逆否命题;
(4)命题:“矩形的两条对角线相等”的逆命题.
其中假命题的个数为( )
| A、0 | B、1 | C、2 | D、3 |
已知O是坐标原点,A,B是直线l:x-y+t=0与圆C:x2+y2=4的两个不同交点,若|
|≤|
+
|,则实数t的取值范围是( )
| AB |
| OA |
| OB |
A、(-2
| ||||
B、[2,2
| ||||
C、(-2
| ||||
D、[-2
|
 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,AC=1,AA1=BC=2.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,AC=1,AA1=BC=2. 如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=
如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=