题目内容
命题“若α=
，则tanα=
”的逆否命题是（ ）
| π |
| 3 |
| 3 |
A、若α≠
| ||||
B、若α=
| ||||
C、若tanα≠
| ||||
D、若tanα=
|
考点：四种命题
专题：简易逻辑
分析：写出命题的条件与结论，根据定义写出逆否命题．
解答：
解：命题的条件是：α=
，
结论是：tanα=
．
∴逆否命题是：若tanα≠
，则α≠
．
故选：C．
| π |
| 3 |
结论是：tanα=
| 3 |
∴逆否命题是：若tanα≠
| 3 |
| π |
| 3 |
故选：C．
点评：本题考查了逆否命题的定义，熟练掌握四种命题的定义是关键．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
在区间[0，6]上随机取一个数x，log2x的值介于1到2之间的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
执行如图所示程序，输出S的值为（ ）
| A、8 | B、26 | C、170 | D、42 |
一个袋中装有大小相同的5个白球和3个红球，现在不放回的取2次球，每次取出一个球，记“第1次拿出的是白球”为事件A，“第2次拿出的是白球”为事件B，则事件A与B同时发生的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设x＞0，y＞0，则（x+y）（
+
）的最小值为（ ）
| 1 |
| x |
| 4 |
| y |
| A、7 | B、8 | C、9 | D、10 |
若抛物线x2=2py（p＞0）的焦点与双曲线
-x2=1的一个焦点重合，则p的值为（ ）
| y2 |
| 3 |
| A、-2 | B、2 | C、-4 | D、4 |
下列说法正确的是（ ）
①若a，b，c∈R且ac2＞bc2，则a＞b；
②若a，b∈R且a＞b，则a3＞b3；
③若a，b∈R且ab≠0，则
+
≥2；
④函数f（x）=x+
（x≠0）的最小值是2．
①若a，b，c∈R且ac2＞bc2，则a＞b；
②若a，b∈R且a＞b，则a3＞b3；
③若a，b∈R且ab≠0，则
| a |
| b |
| b |
| a |
④函数f（x）=x+
| 1 |
| x |
| A、①② | B、②③ | C、③④ | D、①④ |
函数f（x）=2x2-lnx的递减区间是（ ）
A、（0，
| ||||
B、（-
| ||||
C、（
| ||||
D、（-∞，-
|
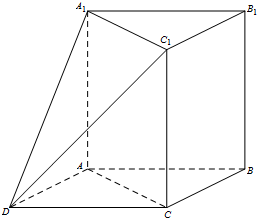如图，在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，∠ACB=90°．以AB，BC为邻边作平行四边形ABCD，连接DA1和DC1．