题目内容
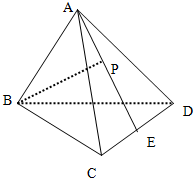已知空间四边形ABCD，BC=BD，AC=AD，E是CD边的中点．在AE上的一个动点P，讨论BP与CD是否存在垂直关系，并证明你的结论．考点：直线与平面垂直的性质
专题：空间位置关系与距离
分析：BP与CD满足垂直关系．由已知条件推导出CD⊥BE，CD⊥AE，从而得到CD⊥平面ABE，由此得到CD⊥BP．
解答：
解：连接BE，BP与CD满足垂直关系．…（2分）
因为BC=BD，E是CD中点，所以CD⊥BE，…（4分）
又因为AC=AD，E是CD中点，所以CD⊥AE，…（6分）
所以CD⊥平面ABE，…（8分）
又因为BP是平面ABE内的直线，
所以CD⊥BP．…（10分）
因为BC=BD，E是CD中点，所以CD⊥BE，…（4分）
又因为AC=AD，E是CD中点，所以CD⊥AE，…（6分）
所以CD⊥平面ABE，…（8分）
又因为BP是平面ABE内的直线，
所以CD⊥BP．…（10分）
点评：本题考查两条直线垂直的判定，是基础题，解题时要注意空间思维能力的培养．
练习册系列答案
全能测控期末小状元系列答案
相关题目
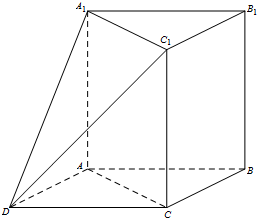如图，在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，∠ACB=90°．以AB，BC为邻边作平行四边形ABCD，连接DA1和DC1． 
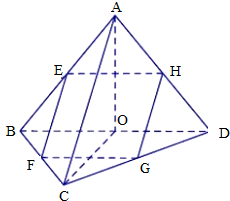在三棱锥A-BCD中，点E、F、G、H分别是AB、BC、CD、DA的中点．