题目内容
函数f（x）=
的导数是（ ）
| 3 | x2 |
| A、3x2 | |||||
B、
| |||||
C、
| |||||
D、-
|
考点：导数的运算
专题：计算题
分析：根据初等函数的导数公式f（x）=xα，则f′（x）=αxα-1，问题得以解决．
解答：
解：f（x）=
=x
∴f′(x)=
x-
=
，
故选：C．
| 3 | x2 |
| 2 |
| 3 |
∴f′(x)=
| 2 |
| 3 |
| 1 |
| 3 |
| 2 | |||
3
|
故选：C．
点评：本题主要考查了初等函数的导数公式，属于基础题．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
函数f（x）=cos2x+
sinxcosx在区间[-
，
]上的最大值为（ ）
| 3 |
| π |
| 4 |
| π |
| 3 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
已知f（x）=
，则
的值是（ ）
| 1 |
| x |
| lim |
| △x→0 |
| -f(2+△x)+f(2) |
| △x |
A、
| ||
| B、2 | ||
C、-
| ||
| D、-2 |
已知圆C：（x-2）2+（y+1）2=3，从点P（-1，-3）发出的光线，经x轴反射后恰好经过圆心C，则入射光线的斜率为（ ）
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知α是第四象限的角，且sinα•cosα=-
，则sinα-cosα=（ ）
| 12 |
| 25 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
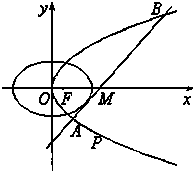已知椭圆C1和抛物线C2有公共焦点F（1，0），C1的中心和C2的顶点都在坐标原点，过点M（4，0）的直线l与抛物线C2分别相交于A，B两点．