题目内容
若函数y=ax+2-2(a>0且a≠1)的图象恒过定点A,若点A在直线
+
=-1上,且m>0,n>0,则m+2n的最小值为( )
| x |
| m |
| y |
| n |
| A、7 | B、8 | C、9 | D、10 |
考点:指数函数的图像变换
专题:函数的性质及应用,不等式的解法及应用
分析:根据指数函数的图象和性质,结合基本不等式的性质即可得到结论.
解答:
解:当x+2=0,解得x=-2,此时y=1-2=-1,
故A(-2,-1),
∵点A在直线
+
=-1上,
∴
+
=1,
于是m+2n=(
+
)(m+2n)=4+
+
≥8,当且仅当
=2,n=2且m=4时等号成立.
故m+2n的最小值为8,
故选:B.
故A(-2,-1),
∵点A在直线
| x |
| m |
| y |
| n |
∴
| 2 |
| m |
| 1 |
| n |
于是m+2n=(
| 2 |
| m |
| 1 |
| n |
| 4n |
| m |
| m |
| n |
| m |
| n |
故m+2n的最小值为8,
故选:B.
点评:本题主要考查指数函数的性质,以及基本不等式的解法,涉及的知识点较多.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).
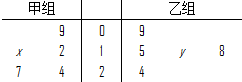
已知甲组数据的平均数为17,乙组数据的中位数为17,则x,y的值分别为( )

已知甲组数据的平均数为17,乙组数据的中位数为17,则x,y的值分别为( )
| A、2,6 | B、2,7 |
| C、3,6 | D、3,7 |
给定命题p:存在x∈R,使
=x
,则
∥
;q:?锐角△ABC,sinA<cosB.下面复合命题中正确的是( )
| a |
| b |
| a |
| b |
| A、p∧q | B、p∨q |
| C、¬p∧q | D、¬p∨q |
已知曲线y=2x2上一点A(2,8),则A处的切线斜率为( )
| A、4 | B、16 | C、8 | D、2 |
函数y=4sin(2x-
)的图象的一个对称中心是( )
| π |
| 6 |
A、(
| ||
B、(
| ||
C、(-
| ||
D、(
|
“a<b<0”是“
>
”的( )条件.
| 1 |
| a |
| 1 |
| b |
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
已知cosα=
,α∈(0,π),则cos(α-
)的值为( )
| 3 |
| 5 |
| π |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=
的导数是( )
| 3 | x2 |
| A、3x2 | |||||
B、
| |||||
C、
| |||||
D、-
|