题目内容
函数f(x)=cos2x+
sinxcosx在区间[-
,
]上的最大值为( )
| 3 |
| π |
| 4 |
| π |
| 3 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
考点:二倍角的正弦,二倍角的余弦
专题:三角函数的求值
分析:利用二倍角公式化简函数的解析式为f(x)=
+sin(
+2x),再结合x的范围,利用正弦函数的定义域和值域求得函数的最大值.
| 1 |
| 2 |
| π |
| 6 |
解答:
解:函数f(x)=cos2x+
sinxcosx=
+
sin2x=
+sin(
+2x),
再根据x∈[-
,
],可得
+2x∈[-
,
],
故当
+2x=
时,函数y取得最大值为
+1=
,
故选:D.
| 3 |
| 1+cos2x |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
再根据x∈[-
| π |
| 4 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
故当
| π |
| 6 |
| π |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
故选:D.
点评:本题主要考查二倍角公式的应用,正弦函数的定义域和值域,属于中档题.

练习册系列答案
相关题目
如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).
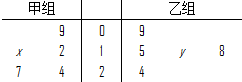
已知甲组数据的平均数为17,乙组数据的中位数为17,则x,y的值分别为( )

已知甲组数据的平均数为17,乙组数据的中位数为17,则x,y的值分别为( )
| A、2,6 | B、2,7 |
| C、3,6 | D、3,7 |
“a<b<0”是“
>
”的( )条件.
| 1 |
| a |
| 1 |
| b |
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
已知cosα=
,α∈(0,π),则cos(α-
)的值为( )
| 3 |
| 5 |
| π |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列函数中,与函数y=x3的值域相同的函数为( )
A、y=(
| ||
| B、y=ln(x+1) | ||
C、y=
| ||
D、y=x+
|
下列命题中,正确命题的个数是( )
(1)若x,y∈C,则x+yi=1+i的充要条件是x=y=1
(2)若a,b∈R且a>b,则a+i>b+i
(3)若x2+y2=0,x,y∈C,则x=y=0.
(1)若x,y∈C,则x+yi=1+i的充要条件是x=y=1
(2)若a,b∈R且a>b,则a+i>b+i
(3)若x2+y2=0,x,y∈C,则x=y=0.
| A、0 | B、1 | C、2 | D、3 |
下列方程所表示的直线中,是函数y=sin(2x+
π)图象的对称轴的是( )
| 5 |
| 2 |
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
D、x=
|
函数f(x)=
的导数是( )
| 3 | x2 |
| A、3x2 | |||||
B、
| |||||
C、
| |||||
D、-
|