题目内容
已知定圆A:(x+1)2+y2=8的圆心为A,动圆M过点B(1,0),且于圆A相切,动圆的圆心M的轨迹的方程为C,
(1)求曲线C的轨迹方程;
(2)直线l过点(0,t)且与曲线C交于P,Q两点,探究:是否存在实数t,使得点N(0,-1)在以PQ为直径的圆上,若存在,请求出t的值;若不存在,请说明理由.
(1)求曲线C的轨迹方程;
(2)直线l过点(0,t)且与曲线C交于P,Q两点,探究:是否存在实数t,使得点N(0,-1)在以PQ为直径的圆上,若存在,请求出t的值;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)依据条件判断定圆和动圆相内切,再依据椭圆的定义写出曲线C的方程;
(2)假设存在实数t,使得点N(0,-1)在以PQ为直径的圆上,联立直线方程和椭圆方程,消去y,得到二次方程,运用韦达定理,判别式大于0,再由直径所对的圆周角为直角,运用直线垂直的条件,化简整理,得到t的方程,解出即可判断.
(2)假设存在实数t,使得点N(0,-1)在以PQ为直径的圆上,联立直线方程和椭圆方程,消去y,得到二次方程,运用韦达定理,判别式大于0,再由直径所对的圆周角为直角,运用直线垂直的条件,化简整理,得到t的方程,解出即可判断.
解答:
解:(1)圆A的圆心为A(-1,0),半径r1=2
,
设动圆M的圆心M(x,y),半径为r2,依题意有,r2=|MB|.
由|AB|=2,可知点B在圆A内,从而圆M内切于圆A,
故|MA|=r1-r2,即|MA|+|MB|=2
,
所以点M的轨迹是以A,B为焦点的椭圆,
设椭圆方程为
+
=1(a>b>0),
由2a=2
,2c=2,可得a2=2,b2=1.
故曲线C的方程为
+y2=1;
(2)假设存在实数t,使得点N(0,-1)在以PQ为直径的圆上.
则由直线l过点(0,t),即有l:y=kx+t,联立椭圆方程x2+2y2=2,
消去y,得,(1+2k2)x2+4ktx+2t2-2=0,设P(x1,y1),Q(x2,y2),
则有△=16k2t2-4(1+2k2)(2t2-2)>0,
x1+x2=-
,x1x2=
,
由于点N(0,-1)在以PQ为直径的圆上,则NP⊥NQ,
即有
•
=-1,即x1x2+(kx1+1+t)(kx2+1+t)=0,
即有(1+k2)x1x2+k(1+t)(x1+x2)+(1+t)2=0,
即有(1+k2)•
+k(t+1)•
+(1+t)2=0,
化简整理,可得3t2+2t-1=0,解得,t=-1,或t=
,
当t=-1时,则直线恒过(0,-1),N与P,Q中某一点重合,只要k≠0,即可;
当t=
时,检验判别式大于0成立,
则存在实数t,使得点N(0,-1)在以PQ为直径的圆上,
且t=-1,或t=
.
| 2 |
设动圆M的圆心M(x,y),半径为r2,依题意有,r2=|MB|.
由|AB|=2,可知点B在圆A内,从而圆M内切于圆A,
故|MA|=r1-r2,即|MA|+|MB|=2
| 2 |
所以点M的轨迹是以A,B为焦点的椭圆,
设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
由2a=2
| 2 |
故曲线C的方程为
| x2 |
| 2 |
(2)假设存在实数t,使得点N(0,-1)在以PQ为直径的圆上.
则由直线l过点(0,t),即有l:y=kx+t,联立椭圆方程x2+2y2=2,
消去y,得,(1+2k2)x2+4ktx+2t2-2=0,设P(x1,y1),Q(x2,y2),
则有△=16k2t2-4(1+2k2)(2t2-2)>0,
x1+x2=-
| 4kt |
| 1+2k2 |
| 2t2-2 |
| 1+2k2 |
由于点N(0,-1)在以PQ为直径的圆上,则NP⊥NQ,
即有
| y1+1 |
| x1 |
| y2+1 |
| x2 |
即有(1+k2)x1x2+k(1+t)(x1+x2)+(1+t)2=0,
即有(1+k2)•
| 2t2-2 |
| 1+2k2 |
| -4kt |
| 1+2k2 |
化简整理,可得3t2+2t-1=0,解得,t=-1,或t=
| 1 |
| 3 |
当t=-1时,则直线恒过(0,-1),N与P,Q中某一点重合,只要k≠0,即可;
当t=
| 1 |
| 3 |
则存在实数t,使得点N(0,-1)在以PQ为直径的圆上,
且t=-1,或t=
| 1 |
| 3 |
点评:本题考查椭圆的定义、方程和性质,考查圆与圆的位置关系,直线方程和椭圆方程联立消去未知数,运用韦达定理,考查化简整理的运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
棱长为1的正方体ABCD-A1B1C1D1及其内部一动点P,集合Q={P||PA|≤1},则集合Q构成的几何图形为( )
| A、圆 | B、四分之一圆 |
| C、球 | D、八分之一球 |
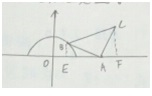 已知B是x2+y2=1(y∈[0,1])上一动点,A(2,0)△ABC是以A为直角顶点的等腰三角形,且A,B,C按顺时针方向排列,则动点C的轨迹方程是
已知B是x2+y2=1(y∈[0,1])上一动点,A(2,0)△ABC是以A为直角顶点的等腰三角形,且A,B,C按顺时针方向排列,则动点C的轨迹方程是