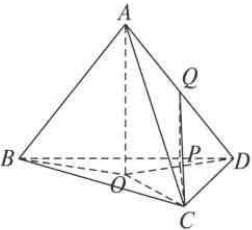
题目内容
一质点P从单位圆O上的点（1，0）出发，以角速度每秒为
弧度逆时针旋转，且与原点O的距离y与时间（单位：秒）的函数关系为y=0.01t+1．
（1）当t=50秒时，求质点P的位置P1的坐标；
（2）当t=32.5分钟时，质点P在位置P2，求S △op1p2的值．
| π |
| 200 |
（1）当t=50秒时，求质点P的位置P1的坐标；
（2）当t=32.5分钟时，质点P在位置P2，求S △op1p2的值．
考点：在实际问题中建立三角函数模型
专题：计算题,三角函数的图像与性质
分析：（1）由题意，求出距离及转过的角，从而求坐标；
（2）求出距离及转过的角，从而可确定△OP1P2为直角三角形，从而求面积．
（2）求出距离及转过的角，从而可确定△OP1P2为直角三角形，从而求面积．
解答：
解：（1）由题意，y=0.01×50+1=1.5，
转过的角为
×50=
，
故质点P的位置P1的坐标中，
x=y=1.5×sin
=
，
故质点P的位置P1的坐标为（
，
）；
（2）t=32.5分钟=32.5×60秒，
y=32.5×60×0.01+1=20.5，
转过的角为
×32.5×60=
=（10π-
），
故△OP1P2为直角三角形，
则S △op1p2=
×1.5×20.5=
．
转过的角为
| π |
| 200 |
| π |
| 4 |
故质点P的位置P1的坐标中，
x=y=1.5×sin
| π |
| 4 |
3
| ||
| 4 |
故质点P的位置P1的坐标为（
3
| ||
| 4 |
3
| ||
| 4 |
（2）t=32.5分钟=32.5×60秒，
y=32.5×60×0.01+1=20.5，
转过的角为
| π |
| 200 |
| 39π |
| 4 |
| π |
| 4 |
故△OP1P2为直角三角形，
则S △op1p2=
| 1 |
| 2 |
| 123 |
| 8 |
点评：本题考查了三角函数的基本应用，属于中档题．
练习册系列答案
相关题目
下列语句是命题的是（ ）
| A、指数函数是增函数吗 | ||
| B、若整数a是素数，则a是奇数 | ||
C、求证
| ||
| D、x＞15 |
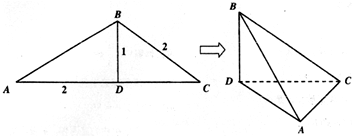
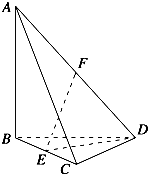如图，四面体ABCD中，AB、BC、BD两两垂直，AB=BC=BD=4，E、F分别为棱BC、AD的中点．