Question

设点P是双曲线

x2

a2

-

y2

b2

=1（a＞0，b＞0）左支上的任意一点，F₁、F₂分别是其左、右焦点，离心率为e，若|

PF1

|=

1

e

•|

PF2

|，则此双曲线的离心率的取值范围是

 

．

Answer 1

考点：双曲线的简单性质

专题：圆锥曲线的定义、性质与方程

分析：设出P点坐标，由双曲线的第二定义得到|

PF1

|=-a-ex0，|

PF2

|=a-ex0，代入|

PF1

|=

1

e

•|

PF2

|后整理，结合P点横坐标的范围得答案．

解答： 解：如图，

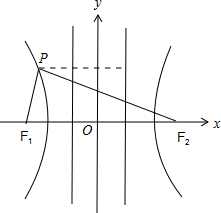
设P（x₀，y₀），
由双曲线的第二定义可得：

| PF1 |

- a2 c -x0

=

| PF2 |

a2 c -x0

=e，
则|

PF1

|=-a-ex0，|

PF2

|=a-ex0，
代入|

PF1

|=

1

e

•|

PF2

|，得-a-ex0=

1

e

(a-ex0)，
即x0=

-ae-a

e2-e

，
由x0=

-ae-a

e2-e

≤-a，得e²-2e-1≤0，
解得：1-

2

≤e≤1+

2

，
由e＞1，
∴1＜e≤1+

2

．
故答案为（1，1+

2

]．

点评：本题考查了双曲线的第二定义，考查了双曲线的几何性质，是中档题．