题目内容
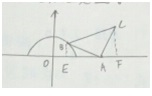已知B是x2+y2=1（y∈[0，1]）上一动点，A（2，0）△ABC是以A为直角顶点的等腰三角形，且A，B，C按顺时针方向排列，则动点C的轨迹方程是考点：轨迹方程
专题：计算题,直线与圆
分析：由题意，设C（x，y），令B（x0，y0），由等腰直角三角形的特征，两直角边垂直且相等建立B，C两点的坐标之间的关系，用点C的坐标，表示出点B的坐标，代入x2+y2=1，整理即可得到点C的轨迹方程．
解答：
解：设C（x，y），令B（x0，y0），
∵点A的坐标为（2，0），△ABC是以BC为斜边的等腰直角三角形，
∴kAB×kAC=-1，且AB=AC
∴
×
=-1①；
（x-2）2+y2=（x0-2）2+y02 ②
由①得x0-2=
代入②得（x-2）2+y2=（
）2+y02，
整理得y02=（x-2）2，又y0＞0，x≥2
可得y0=x-2代入①得
=-1，解得x0=2-y，
又点B（x0，y0）是半圆x2+y2=1（y＞0）上的一个动点，
所以有（x-2）2+（y-2）2=1（x≥2）．
故点C的轨迹方程是（x-2）2+（y-2）2=1（x≥2）．
故答案为：（x-2）2+（y-2）2=1（x≥2）．
∵点A的坐标为（2，0），△ABC是以BC为斜边的等腰直角三角形，
∴kAB×kAC=-1，且AB=AC
∴
| y |
| x-2 |
| y0 |
| x0-2 |
（x-2）2+y2=（x0-2）2+y02 ②
由①得x0-2=
| yy0 |
| x-2 |
| yy0 |
| x-2 |
整理得y02=（x-2）2，又y0＞0，x≥2
可得y0=x-2代入①得
| y |
| x0-2 |
又点B（x0，y0）是半圆x2+y2=1（y＞0）上的一个动点，
所以有（x-2）2+（y-2）2=1（x≥2）．
故点C的轨迹方程是（x-2）2+（y-2）2=1（x≥2）．
故答案为：（x-2）2+（y-2）2=1（x≥2）．
点评：本题考查求轨迹方程，解题的关键是理解题意，运用代入法，本题由垂直与线段相等两个关系建立方程，由于都是符号运算，运算量较大，变形时要严谨，不要因为运算出错，导致解题失败，由解题过程可以看出，此类题求解规律固定，入手一般是从找等量关系开始，切记！
练习册系列答案
相关题目
设M={1，2，5}，N={1，3，6}，那么M∩N等于（ ）
| A、∅ | B、{1，3} |
| C、{1} | D、{2，3} |
下列语句是命题的是（ ）
| A、指数函数是增函数吗 | ||
| B、若整数a是素数，则a是奇数 | ||
C、求证
| ||
| D、x＞15 |
已知数列{an}的前n项之和是Sn，且4Sn=（an+1）2，则下列说法正确的是（ ）
| A、数列{an}为等差数列 |
| B、数列{an}为等比数列 |
| C、数列{an}为等差或等比数列 |
| D、数列{an}可能既不是等差数列也不是等比数列 |