Question

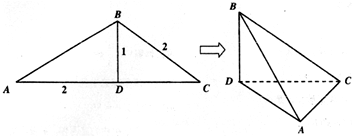
以正方形ABCD的对角线BD为棱折成直二面角，连接AC，求二面角A-CD-B的余弦值．

Answer 1

考点：二面角的平面角及求法

专题：空间位置关系与距离,空间角

分析：由已知可得AO⊥平面BCD，则OC，OA，OD两两互相垂直，以O为原点，建立空间直角坐标系O-xyz，分别求出平面ACD和平面BCD的法向量，代入向量夹角公式，即可得到二面角A-CD-B的余弦值．

解答： 解：∵正方形ABCD的对角线BD为棱折成直二面角，
∴平面ABD⊥平面BCD，
又∵AO⊥BD，平面ABD∩平面BCD=BD，AO?平面ABD
∴AO⊥平面BCD，则OC，OA，OD两两互相垂直，
如图，以O为原点，建立空间直角坐标系O-xyz．

则O（0，0，0），A（0，0，

2

2

），C（

2

2

，0，0），B（0，-

2

2

，0），D（0，

2

2

，0），

OA

=（0，0，

2

2

）是平面BCD的一个法向量．

AC

=（

2

2

，0，-

2

2

），

BC

=（

2

2

，

2

2

，0），
设平面ABC的法向量

n

=（x，y，z），
则

n

•

BC

=0，

n

•

AC

=0．
即

2

2

x-

2

2

z=0，且

2

2

x+

2

2

y=0，
所以y=-x，且z=x，令x=1，则y=-1，z=1，
解得

n

=（1，-1，1）．
从而cos＜

n

，

OA

＞=

| n • OA |

| n |•| OA |

=

3

3

，
二面角A-BC-D的余弦值为

3

3

．

点评：本题考查的知识点是用空间向量求平面间的夹角，直线与平面平行的判定，直线与平面垂直的判定，解答的关键是分别求出平面ACD和平面BCD的法向量．