题目内容
设向量
=(sinx,cosx),
=(sinx,
sinx),x∈R,函数f(x)=
•(
+2
).
(1)求函数f(x)的单调递增区间;
(2)求使不等式f′(x)≥2成立的x的取值集合.
| a |
| b |
| 3 |
| a |
| a |
| b |
(1)求函数f(x)的单调递增区间;
(2)求使不等式f′(x)≥2成立的x的取值集合.
考点:平面向量数量积的坐标表示、模、夹角
专题:三角函数的图像与性质,平面向量及应用
分析:(1)利用数量积运算法则、倍角公式、两角和差的正弦公式、正弦函数的单调性即可得出;
(2)利用导数的运算法则、余弦函数的单调性即可得出.
(2)利用导数的运算法则、余弦函数的单调性即可得出.
解答:
解:(1)函数f(x)=
•(
+2
)=
2+2
•
=sin2x+cos2x+2(sin2x+
sinxcosx)
=1+1-cos2x+
sin2x
=2(
sin2x-
cos2x)+2
=2sin(2x-
)+2.
由2kπ-
≤2x-
≤2kπ+
,
解得kπ-
≤x≤kπ+
(k∈Z),
∴f(x)的单调递增区间为[kπ-
,kπ+
](k∈Z).
(2)由f(x)=2sin(2x-
)+2,得f′(x)=4cos(2x-
).
由f′(x)≥2,得cos(2x-
)≥
,
则2k-
≤2x-
≤2kπ+
,
即kπ-
≤x≤kπ+
(k∈Z).
∴使不等式f′(x)≥2成立的x的取值集合为{x|kπ-
≤x≤kπ+
,k∈Z}.
| a |
| a |
| b |
| a |
| a |
| b |
| 3 |
=1+1-cos2x+
| 3 |
=2(
| ||
| 2 |
| 1 |
| 2 |
=2sin(2x-
| π |
| 6 |
由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解得kπ-
| π |
| 6 |
| π |
| 3 |
∴f(x)的单调递增区间为[kπ-
| π |
| 6 |
| π |
| 3 |
(2)由f(x)=2sin(2x-
| π |
| 6 |
| π |
| 6 |
由f′(x)≥2,得cos(2x-
| π |
| 6 |
| 1 |
| 2 |
则2k-
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
即kπ-
| π |
| 12 |
| π |
| 4 |
∴使不等式f′(x)≥2成立的x的取值集合为{x|kπ-
| π |
| 12 |
| π |
| 4 |
点评:本题考查了数量积运算法则、倍角公式、两角和差的正弦公式、正弦函数的单调性、导数的运算法则、余弦函数的单调性,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
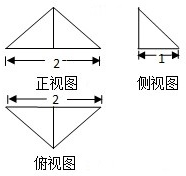 一个几何体的三视图及部分数据如图所示,正视图、侧视图和俯视图都是等腰直角三角形,则该几何体的外接球体积为
一个几何体的三视图及部分数据如图所示,正视图、侧视图和俯视图都是等腰直角三角形,则该几何体的外接球体积为