题目内容
9.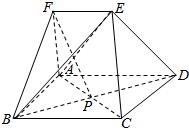 如图,多面体ABCDEF中,四边形ABCD是矩形,EF∥AD,FA⊥面ABCD,AB=AF=EF=1,AD=2,AC交BD于点P
如图,多面体ABCDEF中,四边形ABCD是矩形,EF∥AD,FA⊥面ABCD,AB=AF=EF=1,AD=2,AC交BD于点P(Ⅰ)证明:PF∥面ECD;
(Ⅱ)证明:AE⊥面ECD.
分析 (Ⅰ)取CD中点G,连结EG,PG,推导出四边形EFPG为平行四边形,由此能证明FP∥平面ECD.
(Ⅱ)取AD中点M,连结EM,MC,推导出四边形EFAM为平行四边形,从而EM∥FA,进而EM⊥平面ABCD,CD⊥平面EFAD,由此能证明AE⊥平面ECD.
解答 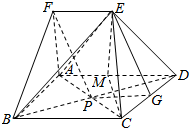 证明:(Ⅰ)取CD中点G,连结EG,PG,
证明:(Ⅰ)取CD中点G,连结EG,PG,
∵点P为矩形ABCD对角线交点,
∴在△ACD中,PG$\underset{∥}{=}$$\frac{1}{2}AD$,
又EF=1,AD=2,EF∥AD,
∴EF$\underset{∥}{=}$PG,∴四边形EFPG为平行四边形,
∴FP∥EG,
又FP?平面ECD,EG?平面ECD,
∴FP∥平面ECD.
(Ⅱ)取AD中点M,连结EM,MC,∴EF=AM=1,EF$\underset{∥}{=}$$\frac{1}{2}AD$,
∴四边形EFAM为平行四边形,∴EM∥FA,
又FA⊥平面ABCD,∴EM⊥平面ABCD,
又MC2=MD2+CD2=2,EM2=1,
∴EC2=MC2+EM2=3,
又AE2=2,AC2=AB2+BC2=1+4=5,
∴AC2=AE2+EC2,∴AE⊥EC,
又CD⊥AD,∴CD⊥平面EFAD,
∴CD⊥AE,又EC∩ED=D,
∴AE⊥平面ECD.
点评 本题考查线面平行的证明,考查线面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
19.已知α∈(0,π)且$cos({\frac{π}{4}+α})=\frac{3}{5}$,则cosα的值为( )
| A. | $\frac{{\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{7\sqrt{2}}}{10}$ | D. | $-\frac{{7\sqrt{2}}}{10}$ |
20.已知x与y之间的一组数据:
则y与x的线性回归方程为$\hat y=bx+a$必过点(2.5,2).
| x | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 7 |
4.下列式子中表示正确的是( )
| A. | 2+cosx=4 | B. | $\sqrt{10}$>π | C. | sinx•cosx=sin2x | D. | sin75°>cos14° |
1.已知顶点为原点,对称轴为坐标轴的抛物线的焦点在直线x-2y-2=0上,则此抛物线的标准方程是( )
| A. | y2=8x | B. | x2=4y | C. | y2=8x或x2=-4y | D. | y2=8x或x2=4y |
18.设fn(x)是等比数列1,x,x2,…,xn的各项和,则fn(2)等于( )
| A. | 2n-1 | B. | 2n+1-1 | C. | 2n-2 | D. | 2n+1-2 |