题目内容
19.已知z1=1+ilog2x,z2=$\sqrt{3}$+i,|z1|<|z2|,则实数x的取值范围为(${2}^{-\sqrt{3}}$,${2}^{\sqrt{3}}$).分析 直接对两个复数求模,解不等式即可.
解答 解:z1=1+ilog2x,z2=$\sqrt{3}$+i,|z1|<|z2|,
∴1+(log2x)2<3+1,
∴|log2x|<$\sqrt{3}$,
∴-$\sqrt{3}$<log2x<$\sqrt{3}$,
∴${2}^{-\sqrt{3}}$<x<${2}^{\sqrt{3}}$,
故x的取值范围为(${2}^{-\sqrt{3}}$,${2}^{\sqrt{3}}$),
故答案为:(${2}^{-\sqrt{3}}$,${2}^{\sqrt{3}}$).
点评 本题考查了复数的求模计算,和解不等式,是基础题.

练习册系列答案
相关题目
10.已知函数f(x)=|log2|x||-($\frac{1}{2}$)x,则下列结论正确的是( )
| A. | f(x)有三个零点,且所有零点之积大于-1 | |
| B. | f(x)有三个零点,且所有零点之积小于-1 | |
| C. | f(x)有四个零点,且所有零点之积大于1 | |
| D. | f(x)有四个零点,且所有零点之积小于1 |
14.已知A(1,-2,11),B(6,-1,4),C(4,2,3),则△ABC为( )
| A. | 锐角三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 钝角三角形 |
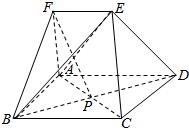 如图,多面体ABCDEF中,四边形ABCD是矩形,EF∥AD,FA⊥面ABCD,AB=AF=EF=1,AD=2,AC交BD于点P
如图,多面体ABCDEF中,四边形ABCD是矩形,EF∥AD,FA⊥面ABCD,AB=AF=EF=1,AD=2,AC交BD于点P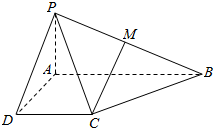 如图,在四棱锥P-ABCD中,已AB∥CD,AB=2DC,M为PB的中点.
如图,在四棱锥P-ABCD中,已AB∥CD,AB=2DC,M为PB的中点.