题目内容
1.已知顶点为原点,对称轴为坐标轴的抛物线的焦点在直线x-2y-2=0上,则此抛物线的标准方程是( )| A. | y2=8x | B. | x2=4y | C. | y2=8x或x2=-4y | D. | y2=8x或x2=4y |
分析 先根据焦点在直线x-2y-2=0上求得焦点的坐标,再分抛物线以x轴对称式和y轴对称式,分别设出抛物线的标准方程,求得p,即可得到抛物线的方程.
解答 解:∵焦点在直线x-2y-2=0上,且抛物线的顶点在原点,对称轴是坐标轴,
焦点的坐标为A(0,-1),或(2,0),
若抛物线以y轴对称式,设方程为x2=-2py,$\frac{p}{2}$=1,求得p=2,∴此抛物线方程为x2=-4y;
若抛物线以x轴对称式,设方程为y2=2px,$\frac{p}{2}$=2,求得p=4,∴此抛物线方程为y2=8x;
故选:C.
点评 本题主要考查了抛物线的性质与方程.属基础题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
11.f(x)是奇函数,对任意的实数x,y,有f(x+y)=f(x)+f(y),且当x<0时,f(x)>0,则f(x)在区间[a,b]上( )
| A. | 有最小值f(a) | B. | 有最大值f(a) | C. | 有最大值$f(\frac{a+b}{2})$ | D. | 有最小值$f(\frac{a+b}{2})$ |
6.某工厂从1970年的年产值200万元增加到40年后2010年的1000万元,假设每年产值增长率相同,则每年年产值增长率是(x为很小的正数时,ln(1+x)≈x,ln5≈1.61)( )
| A. | 3% | B. | 4% | C. | 5% | D. | 6% |
10.已知函数f(x)=|log2|x||-($\frac{1}{2}$)x,则下列结论正确的是( )
| A. | f(x)有三个零点,且所有零点之积大于-1 | |
| B. | f(x)有三个零点,且所有零点之积小于-1 | |
| C. | f(x)有四个零点,且所有零点之积大于1 | |
| D. | f(x)有四个零点,且所有零点之积小于1 |
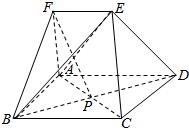 如图,多面体ABCDEF中,四边形ABCD是矩形,EF∥AD,FA⊥面ABCD,AB=AF=EF=1,AD=2,AC交BD于点P
如图,多面体ABCDEF中,四边形ABCD是矩形,EF∥AD,FA⊥面ABCD,AB=AF=EF=1,AD=2,AC交BD于点P