题目内容
19.已知α∈(0,π)且$cos({\frac{π}{4}+α})=\frac{3}{5}$,则cosα的值为( )| A. | $\frac{{\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{7\sqrt{2}}}{10}$ | D. | $-\frac{{7\sqrt{2}}}{10}$ |
分析 根据同角的三角形关系求出sin(α+$\frac{π}{4}$)=$\frac{4}{5}$,再根据cosα=cos(α+$\frac{π}{4}$-$\frac{π}{4}$),利用两角差的余弦公式计算即可.
解答 解:∵α∈(0,π),
∴α+$\frac{π}{4}$∈($\frac{π}{4}$,$\frac{5π}{4}$),
∵$cos({\frac{π}{4}+α})=\frac{3}{5}$,
∴sin(α+$\frac{π}{4}$)=$\frac{4}{5}$,
∴cosα=cos(α+$\frac{π}{4}$-$\frac{π}{4}$)=cos(α+$\frac{π}{4}$)cos$\frac{π}{4}$+sin(α+$\frac{π}{4}$)sin$\frac{π}{4}$=$\frac{3}{5}$×$\frac{\sqrt{2}}{2}$+$\frac{4}{5}$×$\frac{\sqrt{2}}{2}$=$\frac{7\sqrt{2}}{10}$,
故选:C.
点评 本题考查了同角的三角函数的关系以及两角差的余弦公式,培养了学生的转化能力和计算能力,属于基础题.

练习册系列答案
相关题目
9.已知集合A={1,2},B={1,m,3},如果A∩B=A,那么实数m等于( )
| A. | -1 | B. | 0 | C. | 2 | D. | 4 |
10.已知集合M={x|-1<x<4},N={x|-2<x<1},则M∩N=( )
| A. | (-1,4) | B. | (-1,1) | C. | (-2,4) | D. | [-1,1] |
11.f(x)是奇函数,对任意的实数x,y,有f(x+y)=f(x)+f(y),且当x<0时,f(x)>0,则f(x)在区间[a,b]上( )
| A. | 有最小值f(a) | B. | 有最大值f(a) | C. | 有最大值$f(\frac{a+b}{2})$ | D. | 有最小值$f(\frac{a+b}{2})$ |
8.已知a=log${\;}_{\frac{1}{2}}$5,b=log23,c=1,d=3-0.6,那么( )
| A. | a<c<b<d | B. | a<d<c<b | C. | a<b<c<d | D. | a<c<d<b |
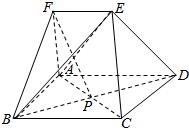 如图,多面体ABCDEF中,四边形ABCD是矩形,EF∥AD,FA⊥面ABCD,AB=AF=EF=1,AD=2,AC交BD于点P
如图,多面体ABCDEF中,四边形ABCD是矩形,EF∥AD,FA⊥面ABCD,AB=AF=EF=1,AD=2,AC交BD于点P