题目内容
18.设fn(x)是等比数列1,x,x2,…,xn的各项和,则fn(2)等于( )| A. | 2n-1 | B. | 2n+1-1 | C. | 2n-2 | D. | 2n+1-2 |
分析 由已知得∴fn(2)=1+2+22+…+2n,由此利用等比数列性质能求出结果.
解答 解:∵fn(x)是等比数列1,x,x2,…,xn的各项和,
∴fn(2)=1+2+22+…+2n
=$\frac{1-{2}^{n+1}}{1-2}$=2n+1-1.
故选:B.
点评 本题考查等比数列的前n项和的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
8.已知a=log${\;}_{\frac{1}{2}}$5,b=log23,c=1,d=3-0.6,那么( )
| A. | a<c<b<d | B. | a<d<c<b | C. | a<b<c<d | D. | a<c<d<b |
6.某工厂从1970年的年产值200万元增加到40年后2010年的1000万元,假设每年产值增长率相同,则每年年产值增长率是(x为很小的正数时,ln(1+x)≈x,ln5≈1.61)( )
| A. | 3% | B. | 4% | C. | 5% | D. | 6% |
10.已知函数f(x)=|log2|x||-($\frac{1}{2}$)x,则下列结论正确的是( )
| A. | f(x)有三个零点,且所有零点之积大于-1 | |
| B. | f(x)有三个零点,且所有零点之积小于-1 | |
| C. | f(x)有四个零点,且所有零点之积大于1 | |
| D. | f(x)有四个零点,且所有零点之积小于1 |
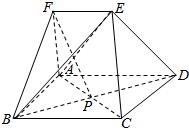 如图,多面体ABCDEF中,四边形ABCD是矩形,EF∥AD,FA⊥面ABCD,AB=AF=EF=1,AD=2,AC交BD于点P
如图,多面体ABCDEF中,四边形ABCD是矩形,EF∥AD,FA⊥面ABCD,AB=AF=EF=1,AD=2,AC交BD于点P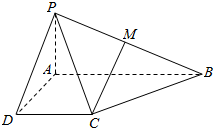 如图,在四棱锥P-ABCD中,已AB∥CD,AB=2DC,M为PB的中点.
如图,在四棱锥P-ABCD中,已AB∥CD,AB=2DC,M为PB的中点.