题目内容
14.若函数f(x)=a•2x+2-x为偶函数,则实数a的值是1.分析 根据函数奇偶性的定义建立方程关系进行求解即可.
解答 解:∵f(x)=a•2x+2-x为偶函数,
∴f(-x)=f(x),
即a•2-x+2x=a•2x+2-x,
即a•(2-x-2x)=2-x-2x,
则a=1,
故答案为:1.
点评 本题主要考查函数奇偶性的应用,根据条件建立方程关系是解决本题的关键,比较基础.

练习册系列答案
相关题目
5.已知抛物线的顶点在原点,焦点在y轴上,其上的点P(m,-3)到焦点的距离为5,則抛物线方程为( )
| A. | x2=8y | B. | x2=4y | C. | x2=-4y | D. | x2=-8y |
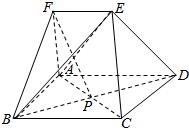 如图,多面体ABCDEF中,四边形ABCD是矩形,EF∥AD,FA⊥面ABCD,AB=AF=EF=1,AD=2,AC交BD于点P
如图,多面体ABCDEF中,四边形ABCD是矩形,EF∥AD,FA⊥面ABCD,AB=AF=EF=1,AD=2,AC交BD于点P