题目内容
设函数f(x)=|x-1|+|2x+1|
(Ⅰ)解不等式f(x)<3;
(Ⅱ)若不等式f(x)≤|
a-1|解集非空,求a的取值范围.
(Ⅰ)解不等式f(x)<3;
(Ⅱ)若不等式f(x)≤|
| 1 |
| 2 |
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)令y=|x-1|+|2x+1|,对自变量x分类讨论,去掉绝对值符号,解相应的不等式f(x)<3即可;
(Ⅱ)由(Ⅰ)知f(x)的最小值为
,依题意,解不等式需
≤|
a-1|即可.
(Ⅱ)由(Ⅰ)知f(x)的最小值为
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
解答:
解:(Ⅰ)令y=|x-1|+|2x+1|,则y=
,
∵y<3,
∴-1<x<1…(5分)
(Ⅱ)由(Ⅰ)知f(x)的最小值为
,所以只需
≤|
a-1|,
解得:a≥5或a≤-1,
∴a的取值范围是(-∞,-1]∪[5,+∞)…(10分)
|
∵y<3,
∴-1<x<1…(5分)
(Ⅱ)由(Ⅰ)知f(x)的最小值为
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
解得:a≥5或a≤-1,
∴a的取值范围是(-∞,-1]∪[5,+∞)…(10分)
点评:本题考查绝对值不等式的解法,考查等价转化思想与分类讨论思想的应用,考查理解与运算能力,属于中档题.

练习册系列答案
相关题目
已知实数x,y满足
,则z=x+2y的最大值为( )
|
| A、-3 | B、21 | C、3 | D、24 |
 如图,圆O的两弦AB和CD交于点E,EF∥CB,EF交AD的延长线于点F.求证:△DEF∽△EAF.
如图,圆O的两弦AB和CD交于点E,EF∥CB,EF交AD的延长线于点F.求证:△DEF∽△EAF.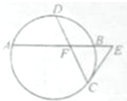 如图,已知圆中两条弦AB与CD相交于点F,且DF=CF=
如图,已知圆中两条弦AB与CD相交于点F,且DF=CF=