题目内容
2.函数f(x)=|x2-2x-3|的增区间是[-1,1],[3,+∞).分析 由题意画出图形,结合图象得答案.
解答 解:作出函数f(x)=|x2-2x-3|的图象如图,
由图可知,函数的增区间为[-1,1],[3,+∞).
故答案为:[-1,1],[3,+∞).
点评 本题考查复合函数的单调性,考查了数形结合的解题思想方法,是基础题.

练习册系列答案
相关题目
12.有5本不同的书,其中语文书2本,数学书2本,物理书1本,若从中任抽一本,抽到的书是数学书的概率是( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
10.在下列直线中,与直线x+3y一4=0相交的直线为( )
| A. | x+3y=0 | B. | y=-$\frac{1}{3}x$-12 | C. | $\frac{x}{2}+\frac{y}{3}$=1 | D. | y=-$\frac{1}{3}$x+4 |
17.已知$\overrightarrow{a}$=(2,-1),$\overrightarrow{b}$=(m,3),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则m=( )
| A. | -$\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | -6 | D. | 6 |
11.已知点A(1,0,0),B(0,1,0),C(0,0,1),点D满足条件:DB⊥AC,DC⊥AB,AD=BC,则点D的坐标为( )
| A. | (1,1,1) | B. | (-1,-1,-1)或($\frac{1}{3}$,$\frac{1}{3}$,$\frac{1}{3}$) | ||
| C. | ($\frac{1}{3}$,$\frac{1}{3}$,$\frac{1}{3}$) | D. | (1,1,1)或(-$\frac{1}{3}$,-$\frac{1}{3}$,-$\frac{1}{3}$) |
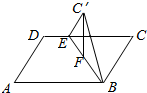 已知矩形ABCD的边长AB=6,AD=4,在CD上截取CE=4,以BE为棱将△BCE折成△BC1E,使△BC1E的高C1F⊥平面ABED,则点C1到AB的距离为2$\sqrt{3}$.
已知矩形ABCD的边长AB=6,AD=4,在CD上截取CE=4,以BE为棱将△BCE折成△BC1E,使△BC1E的高C1F⊥平面ABED,则点C1到AB的距离为2$\sqrt{3}$.