题目内容
12.判断下列函数是否具有奇偶性:(1)f(x)=x+x3+x5;
(2)f(x)=x2,x∈(-1,3);
(3)f(x)=-x2;
(4)f(x)=5x+2;
(5)f(x)=(x+1)(x-1).
分析 根据函数奇偶性的定义,逐一分析给定函数的奇偶性,可得答案.
解答 解:(1)函数f(x)=x+x3+x5的定义域为R,关于原点对称,
且f(-x)=-f(x)恒成立,故函数f(x)=x+x3+x5为奇函数;
(2)f(x)=x2,x∈(-1,3)的定义域不关于原点对称,
故函数f(x)=x2,x∈(-1,3)为非奇非偶函数;
(3)f(x)=-x2的定义域为R,关于原点对称,
且f(-x)=f(x)恒成立,故函数f(x)=-x2为偶函数;
(4)f(x)=5x+2的定义域为R,关于原点对称,
但f(-x)=f(x)与f(-x)=-f(x)均不恒成立,故函数f(x)=5x+2为非奇非偶函数;
(5)f(x)=(x+1)(x-1)=x2-1的定义域为R,关于原点对称,
且f(-x)=f(x)恒成立,故函数f(x)=(x+1)(x-1)为偶函数.
点评 本题考查的知识点是函数奇偶性的性质,熟练掌握函数奇偶性的判定方法,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知A={x|-1<x<2},B={x|x≤1},则A∩(∁RB)=( )
| A. | {x|1<x<2} | B. | {x|-1<x<1} | C. | {x|-1<x<2} | D. | {x|1≤x<2} |
4.函数y=$\sqrt{{x}^{2}-2x-3}$的定义域为( )
| A. | [-1,3] | B. | (-∞,-1)∪(3,+∞) | C. | (-1,3) | D. | (-∞,-1]∪[3,+∞) |
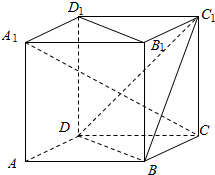 如图,ABCD-A1B1C1D1是棱长为1正方体.
如图,ABCD-A1B1C1D1是棱长为1正方体.