题目内容
7.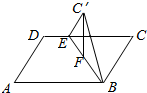 已知矩形ABCD的边长AB=6,AD=4,在CD上截取CE=4,以BE为棱将△BCE折成△BC1E,使△BC1E的高C1F⊥平面ABED,则点C1到AB的距离为2$\sqrt{3}$.
已知矩形ABCD的边长AB=6,AD=4,在CD上截取CE=4,以BE为棱将△BCE折成△BC1E,使△BC1E的高C1F⊥平面ABED,则点C1到AB的距离为2$\sqrt{3}$.
分析 过F点作FG⊥AB于G,连接C′G,FG,由三垂线定理可得C′G为C′到边AB的距离,进而根据勾股定理,即可求出答案.
解答  解:∵C′F⊥平面ABED,BE?平面ABED
解:∵C′F⊥平面ABED,BE?平面ABED
∴CF⊥BE
∴在对折前CF⊥BE
由BC=,CE=4,
∴CF=2$\sqrt{2}$,
∴点C′到平面ABED的距离点C′F到平面ABED的距离=2$\sqrt{2}$,
过F点作FG⊥AB于G,连接C′G,FG,
由三垂线定理,可得C′G⊥AB
即C′G为C′到边AB的距离
易得F为BE的中点,
则FG=$\frac{1}{2}$BC=2,又由C′F=2$\sqrt{2}$,
∴C′G=2$\sqrt{3}$,
故答案为:2$\sqrt{3}$
点评 本题考查的知识点是空间点到点的距离,点到面的距离,其中添加辅助线,将空间距离问题,转化为解三角形问题,是解答本题的关键.

练习册系列答案
相关题目
17.已知数列{an}满足an=$\left\{\begin{array}{l}{(1-2a)n+1,n>3}\\{{a}^{n-2},1≤n≤3}\end{array}\right.$(n∈N*),若对于任意的n∈N*都有an>an+1,则实数a的取值范围是( )
| A. | (0,$\frac{1}{2}$) | B. | (0,$\frac{5}{9}$) | C. | ($\frac{1}{2}$,$\frac{5}{9}$) | D. | ($\frac{5}{9}$,1) |
15.已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,<$\overrightarrow{a}$,$\overrightarrow{b}$>=60°,则$\overrightarrow{a}$•$\overrightarrow{b}$=( )
| A. | 6 | B. | 3 | C. | 6$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
17.已知A={x|-1<x<2},B={x|x≤1},则A∩(∁RB)=( )
| A. | {x|1<x<2} | B. | {x|-1<x<1} | C. | {x|-1<x<2} | D. | {x|1≤x<2} |
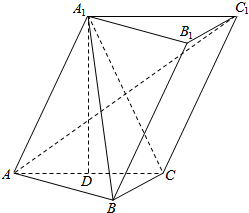 已知三棱柱ABC-A1B1C1,A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,又知BA1⊥AC1
已知三棱柱ABC-A1B1C1,A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,又知BA1⊥AC1