题目内容
11.已知点A(1,0,0),B(0,1,0),C(0,0,1),点D满足条件:DB⊥AC,DC⊥AB,AD=BC,则点D的坐标为( )| A. | (1,1,1) | B. | (-1,-1,-1)或($\frac{1}{3}$,$\frac{1}{3}$,$\frac{1}{3}$) | ||
| C. | ($\frac{1}{3}$,$\frac{1}{3}$,$\frac{1}{3}$) | D. | (1,1,1)或(-$\frac{1}{3}$,-$\frac{1}{3}$,-$\frac{1}{3}$) |
分析 利用验证法,通过向量数量积为0,向量的模是否相等判断即可.
解答 解:点A(1,0,0),B(0,1,0),C(0,0,1),
当D为(1,1,1)时,$\overrightarrow{AC}$=(-1,0,1),$\overrightarrow{AB}$=(-1,1,0),$\overrightarrow{BC}$=(0,-1,1),
$\overrightarrow{DB}$=(-1,0,-1),$\overrightarrow{DC}$=(-1,-1,0),$\overrightarrow{AD}$=(0,1,1).
$\overrightarrow{DB}•\overrightarrow{AC}$=0,$\overrightarrow{DC}•\overrightarrow{AB}$=0,并且满足AD=BC,所以(1,1,1)可以是D的坐标.
如果D为($\frac{1}{3}$,$\frac{1}{3}$,$\frac{1}{3}$)时,$\overrightarrow{AC}$=(-1,0,1),$\overrightarrow{AB}$=(-1,1,0),$\overrightarrow{BC}$=(0,-1,1),
$\overrightarrow{DB}$=(-$\frac{1}{3}$,$\frac{2}{3}$,-$\frac{1}{3}$),$\overrightarrow{DC}$=(-$\frac{1}{3}$,-$\frac{1}{3}$,$\frac{2}{3}$),$\overrightarrow{AD}$=($-\frac{2}{3}$,$\frac{1}{3}$,$\frac{1}{3}$).
$\overrightarrow{DB}•\overrightarrow{AC}$=0,$\overrightarrow{DC}•\overrightarrow{AB}$=0,并且不满足AD=BC,所以D的坐标不能为($\frac{1}{3}$,$\frac{1}{3}$,$\frac{1}{3}$).
故选:A.
点评 本题考查了向量的模、向量数量积运算,考查了计算能力,属于基础题.

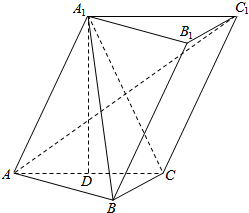 已知三棱柱ABC-A1B1C1,A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,又知BA1⊥AC1
已知三棱柱ABC-A1B1C1,A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,又知BA1⊥AC1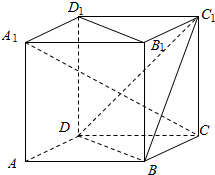 如图,ABCD-A1B1C1D1是棱长为1正方体.
如图,ABCD-A1B1C1D1是棱长为1正方体.