题目内容
14．函数f（x）=lg（2x-1），x∈[1，log211）的值域为[0，1）．分析 由x的范围求出2x-1范围，再由对数函数的单调性求得原函数值域．
解答 解：由x∈[1，log211），得2x∈[2，11），
则2x-1∈[1，10），
∴lg（2x-1）∈[0，1）．
故答案为：[0，1）．
点评 本题考查函数的值域的求法，考查了指数函数和对数函数的单调性，是基础的计算题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．
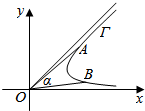如图，在平面直角坐标系xOy中，对于曲线Γ，若存在以O为顶点的角α，使得α≥∠AOB对于曲线π上的任意两个不同的点A，B恒成立，则称角α为曲线的相对于点O的“渐近角”并称其中最小的“渐近角”为曲线Γ的相对于点O的“望角”．已知曲线C：y=$\left\{\begin{array}{l}{2x{e}^{x-1}+2，x＞0}\\{\frac{\sqrt{36+25{x}^{2}}}{3}，x≤0}\end{array}\right.$（其中e=2.71828…是自然对数的底数），则曲线C的相对于点O的“望角”为（ ）
如图，在平面直角坐标系xOy中，对于曲线Γ，若存在以O为顶点的角α，使得α≥∠AOB对于曲线π上的任意两个不同的点A，B恒成立，则称角α为曲线的相对于点O的“渐近角”并称其中最小的“渐近角”为曲线Γ的相对于点O的“望角”．已知曲线C：y=$\left\{\begin{array}{l}{2x{e}^{x-1}+2，x＞0}\\{\frac{\sqrt{36+25{x}^{2}}}{3}，x≤0}\end{array}\right.$（其中e=2.71828…是自然对数的底数），则曲线C的相对于点O的“望角”为（ ）| A． | $\frac{3π}{4}$ | B． | $\frac{2π}{3}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{4}$ |
9．若复数z满足（3+4i）z=|3-4i|，其中i为虚数单位，则z的虚部为（ ）
| A． | -$\frac{4}{5}$ | B． | $\frac{4}{5}$ | C． | 4 | D． | -4 |
4．函数y=$\sqrt{{x}^{2}-2x-3}$的定义域为（ ）
| A． | [-1，3] | B． | （-∞，-1）∪（3，+∞） | C． | （-1，3） | D． | （-∞，-1]∪[3，+∞） |