题目内容
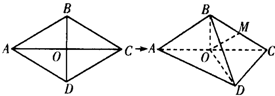如图，平面四边形ABCD中，AB=BC=CD=DA=BD=6，O为AC，BD的交点．将四边形ABCD沿对角线AC折起，得到三棱锥B-ACD，且BD=3| 2 |
（Ⅰ）若M点是BC的中点，求证：OM∥平面ABD；
（Ⅱ）求二面角A-BD-O的余弦值．
考点：用空间向量求平面间的夹角,直线与平面平行的判定
专题：空间位置关系与距离,空间角,空间向量及应用
分析：（Ⅰ）根据已知条件知O为AC中点，所以OM∥AB，从而根据线面平行的判定定理得到OM∥平面ABD；
（Ⅱ）根据已知条件可得到∠BOD=90°，从而得到三条直线OD，OC，OB两两垂直，从而可分别以这三条直线为x，y，z轴建立空间直角坐标系．取BD中点E，连接OE，AE，便可说明∠AEO是二面角A-BD-O的平面角，而∠AEO等于向量
，
的夹角，所以求向量
，
的坐标，代入两向量夹角的余弦公式求cos∠AEO即可．
（Ⅱ）根据已知条件可得到∠BOD=90°，从而得到三条直线OD，OC，OB两两垂直，从而可分别以这三条直线为x，y，z轴建立空间直角坐标系．取BD中点E，连接OE，AE，便可说明∠AEO是二面角A-BD-O的平面角，而∠AEO等于向量
| OE |
| AE |
| OE |
| AE |
解答：
解：（Ⅰ）根据已知条件知四边形ABCD是菱形，O是AC中点；
又M点是BC中点，∴OM是△ABC的中位线；
∴OM∥AB，AB?平面ABD，OM?平面ABD；
∴OM∥平面ABD；
（Ⅱ）如图，根据已知OB=OD=3，BD=3
；
∴∠BOD=90°，即OB⊥OD，又由已知条件OD⊥OC，OC⊥OB；
∴OD，OC，OB三条直线两两垂直，所以分别以这三条直线为x轴，y轴，z轴建立如图所示空间直角坐标系；
则能确定以下几点坐标：
O（0，0，0），A（（0，-3
，0），B（0，0，3），D（3，0，0）；
取BD中点E并连接OE，AE，∵OB=OD，AB=AD；
∴BD⊥OE，BD⊥AE；
∴∠AEO是二面角A-BD-O的平面角，∠AEO等于向量
，
的夹角；
E（
，0，
），
=(
，0，
)，
=(
，3
，
)；
∴cos∠AEO=
=
=
；
∴二面角A-BD-O的余弦值为
．
又M点是BC中点，∴OM是△ABC的中位线；
∴OM∥AB，AB?平面ABD，OM?平面ABD；
∴OM∥平面ABD；
（Ⅱ）如图，根据已知OB=OD=3，BD=3
| 2 |
∴∠BOD=90°，即OB⊥OD，又由已知条件OD⊥OC，OC⊥OB；∴OD，OC，OB三条直线两两垂直，所以分别以这三条直线为x轴，y轴，z轴建立如图所示空间直角坐标系；
则能确定以下几点坐标：
O（0，0，0），A（（0，-3
| 3 |
取BD中点E并连接OE，AE，∵OB=OD，AB=AD；
∴BD⊥OE，BD⊥AE；
∴∠AEO是二面角A-BD-O的平面角，∠AEO等于向量
| OE |
| AE |
E（
| 3 |
| 2 |
| 3 |
| 2 |
| OE |
| 3 |
| 2 |
| 3 |
| 2 |
| AE |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
∴cos∠AEO=
| ||||
|
|
| ||||
|
| ||
| 7 |
∴二面角A-BD-O的余弦值为
| ||
| 7 |
点评：考查线面平行的判定定理，通过建立空间直角坐标系，利用向量求二面角的方法，以及二面角的平面角的概念，两向量夹角的余弦公式的坐标运算．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
若从区间（0，e）内随机取两个数，则这两个数之积不小于e的概率为（ ）
A、1-
| ||
B、1-
| ||
C、
| ||
D、
|
已知全集U={x∈Z|x2-9x+8＜0}，M={3，5，6}，N={x|x2-9x+20=0}，则集合{2，7}为（ ）
| A、M∪N |
| B、M∩N |
| C、∁U（M∪N） |
| D、∁U（M∩N） |
设α∈(0，
)，β∈(0，
)，且tanα=
，则下列结论中正确的是（ ）
| π |
| 2 |
| π |
| 4 |
| 1+sin2β |
| cos2β |
A、2α-β=
| ||
B、2α+β=
| ||
C、α-β=
| ||
D、α+β=
|
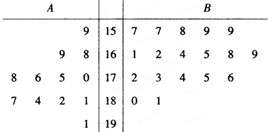某园艺师培育了两种珍稀树苗A与B，株数分别为12与18，现将这30株树苗的高度编写成茎叶图如图（单位：cm）若树高在175cm以上（包括175cm）定义为“生长良好”，树高在175cm以下（不包括175cm）定义为“非生长良好”，且只有“B生长良好”的才可以出售．