题目内容
设0<m<
,若
+
≥k恒成立,则实数k的最大值是 .
| 1 |
| 2 |
| 1 |
| m |
| 8 |
| 1-2m |
考点:利用导数求闭区间上函数的最值,基本不等式
专题:导数的综合应用
分析:利用导数研究函数的单调性极值最值即可得出.
解答:
解:令f(m)=
+
,0<m<
,
f′(m)=-
+
=
,
令f′(m)=0,解得m=
.
令f′(m)>0,解得0<m<
,此时函数f(m)单调递增;令f′(m)<0,解得
<m<
,此时函数f(m)单调递减.
∴当m=
时,函数f(m)取得极大值即最大值18.
故答案为:18.
| 1 |
| m |
| 8 |
| 1-2m |
| 1 |
| 2 |
f′(m)=-
| 1 |
| m2 |
| 16 |
| (1-2m)2 |
| -(6m-1)(2m+1) |
| m2(2m-1)2 |
令f′(m)=0,解得m=
| 1 |
| 6 |
令f′(m)>0,解得0<m<
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 2 |
∴当m=
| 1 |
| 6 |
故答案为:18.
点评:本题考查了导数研究函数的单调性极值最值,属于基础题.

练习册系列答案
相关题目
抛物线y2=4x上与焦点相距最近的点的坐标是( )
| A、(0,0) |
| B、(1,2) |
| C、(1,-2) |
| D、以上都不是 |
若Sn是等差数列{an}的前n项和,且S8-S4=12,则S12的值为( )
| A、22 | B、36 | C、44 | D、64 |
| ∫ | 2π 0 |
| A、0 | B、2 | C、4 | D、2π |
不等式“||x-1|≥1是”是“1og2x>1”成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
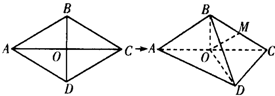 如图,平面四边形ABCD中,AB=BC=CD=DA=BD=6,O为AC,BD的交点.将四边形ABCD沿对角线AC折起,得到三棱锥B-ACD,且BD=3
如图,平面四边形ABCD中,AB=BC=CD=DA=BD=6,O为AC,BD的交点.将四边形ABCD沿对角线AC折起,得到三棱锥B-ACD,且BD=3